Numeracy, Maths and Statistics - Academic Skills Kit

Polar Form and De Moivre's Theorem

ContentsToggle Main Menu 1 Definition1.1 Polar Form1.2 De Moivre's Theorem 2 Worked Examples 3 Workbooks 4 See Also 5 External Resources

Definition

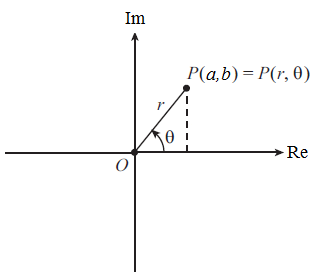
Polar Form

In addition to the Cartesian form, $z=a+bi$ , complex numbers can also be written in trigonometric polar form where $r$ is the modulus and $\theta$ is the argument of the number, in radians.

You may see $\mathrm{cis} \theta$ used in calculations with complex numbers - this is a shorthand for $\cos \theta + i \sin \theta$ .

|center

See the page on Modulus and Argument for a full description of the calculation of $r$ and $\theta$ .

Recall Euler's formula, which relates exponentials and trigonometric formulae.

$e^{i \theta} = \cos \theta + i \sin \theta$

Using this, we can also write complex numbers in exponential polar form

$z = r e^{i \theta}$

The angle notation is often used in electronics: $z = r\angle \theta$

De Moivre's Theorem

De Moivre's theorem states that for any complex number $z = \cos \theta + i \sin \theta$ and integer $n$ , $(\cos \theta + i\sin \theta)^n = \cos(n\theta)+i\sin(n\theta)$ This can be stated in exponential polar form as $( e^{i\theta})^n= e^{in\theta}$

De Moivre's theorem is useful when finding a power of a complex number. To apply the theorem to a complex number, first convert it to polar form, then apply the identity given in the theorem: $\begin{align} (a+bi)^n &= \bigl(r(\cos \theta + i\sin \theta)\bigr)^n \\ &= r^n \cdot (\cos \theta + i\sin \theta)^n \\ &= r^n\bigl(\cos(n\theta)+i\sin(n\theta)\bigr) \end{align}$

Worked Examples

Example 1

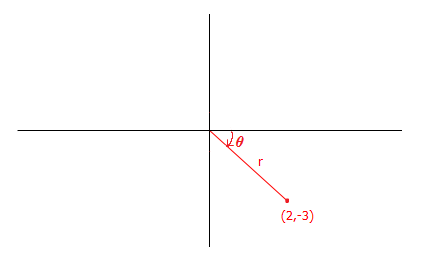
Express the complex number $z=2-3i$ in polar form.

Solution

Find the modulus and the argument.

$r = \lvert z \rvert = \sqrt{2^2+(-3)^2} = \sqrt{13}$

$\theta = \arg z = \tan^{-1}\left(\dfrac{-3}{2}\right) = -0.98 \text{ radians (to 2 d.p.)}$

Note: Remember to check that the value for $\theta$ is correct by drawing an Argand diagram. See Modulus and Argument for more detail on finding the argument.

In exponential polar form, $z = \sqrt{13} e^{-0.98i}$

Or, in trigonometic polar form, $z = \sqrt{13}\bigl(\cos(-0.98) + i\sin(-0.98)\bigr)$

Example 2

Use De Moivre's Theorem to compute $(-1+4i)^{4}$ .

Solution

First, find the modulus. $\begin{align} \lvert -1+4i \rvert & = \sqrt{(-1)^2 + 4^2}\\ &= \sqrt{17} \end{align}$

Then find the argument. If we are not careful then we could calculate as follows: $\begin{align} \arg(-1+4i) &= \tan^{-1}\left(\frac{4}{-1}\right)\\ &= \tan^{-1}(-4)\\ &= -1.33 \end{align}$

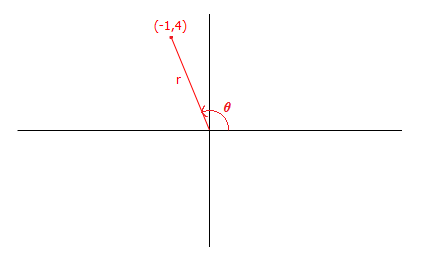
But the angle $\theta = -1.33$ radians lies in the fourth quadrant and we see that it does not correspond with the point $(-1,4)$ , which lies in the second quadrant. We must add $\pi$ to this to correct it. See Modulus and Argument for a full discussion and plenty of examples.

So the actual value for $\theta$ is: $\theta = \pi + \tan^{-1}(-4)=1.82 \text{ radians (to 2 d.p.)}$

Now we can write the complex number in polar form. $(-1+4i) = \sqrt{17}(\cos 1.82 + i \sin 1.82)$

So $\begin{align} (-1+4i)^{4} &= \bigl(\sqrt{17}(\cos 1.82+ i\sin 1.82)\bigr)^{4}\\ &= (\sqrt{17})^{4} \times \bigl(\cos 1.82 + i\sin 1.82)\bigr)^{4}\\ &= 17^2 \times \bigl( \cos (4 \times 1.82)+i\sin (4 \times 1.82)\bigr) & \text{ (by De Moivre's theorem)}\\ &=289\bigl(\cos 7.28 + i \sin 7.28\bigr) \text{ in polar form, or}\\ &=156.9 +242.7i \text{ (to 1 d.p.)} \end{align}$

Workbooks

These workbooks produced by HELM are good revision aids, containing key points for revision and many worked examples.

External Resources

The exponential form workbook at mathcentre.
Trigonometric polar form workbook at mathcentre.
The polar form of a complex number leaflet at mathcentre.