Solution

This graph shows the lines $f(x)=3x-6$, in red, and $g(x)=4-2x$, in blue. We are looking for the values of $x$ for which the red line is greater than the blue line.

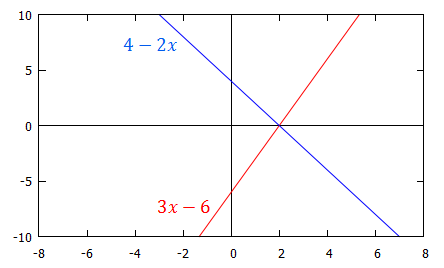
|center

\[3x-6 \geq 4-2x\] Add $6$ to both sides. \[3x \geq 10-2x\] Add $2x$ to both sides. \[5x\geq 10\] Divide through by $5$. As this is a positive number, the inequality symbol remains unchanged. \[x \geq \frac{10}{5} = 2\]

Hence the solutions to this inequality are all $x$ such that $x \geq 2$ i.e. the interval $[2,\infty)$. This agrees with the graph.

Solution

This is the graph of $f(x)=x^2-2x-8$. When the curve is above the $x$ axis, this satisfies part (a) of the question. When the curve is below the $x$-axis, this satisfies part (b).

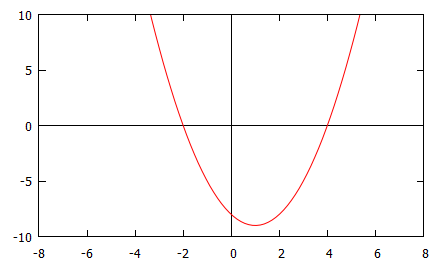
|center

First factorise the expression.

\[x^2-2x-8 = (x-4)(x+2)\]

This is zero at $x=4$ and $x=-2$, so these are the points at which the curve crosses the $x$-axis.

(a) For $x^2-2x-8\gt0$, we have \[(x-4)(x+2) \gt 0\]

For the product on the left hand side be greater than zero, both brackets must give positive answers, or both brackets must give negative answers.

To make positive brackets, we must have $x\gt 4$ and $x \gt -2$. $x\gt 4$ satisfies both these conditions.

To make negative brackets, we must have $x \lt 4$ and $x \lt -2$, and $x\lt -2$ satisfies both these conditions.

So we must have

\[x\lt-2 \text{ or } x\gt4\]

In set notation, this is the union of intervals \[[-\infty, -2) \cup (4,\infty].\]

(b) For $x^2-2x-8\lt0$, we have \[(x-4)(x+2) \lt 0\] For this to be less than zero, we must have one negative bracket and one positive bracket.

We cannot make the first bracket positive and the second negative as we would need $x\gt 4$ and $x\lt -2$, which cannot happen at the same time.

To make the first bracket negative and second positive, we must have $x\lt 4$ and $x \gt -2$, so our answer is \[-2 \lt x \lt 4\]

In set notation, this is the interval \[(-2,4).\]

solution

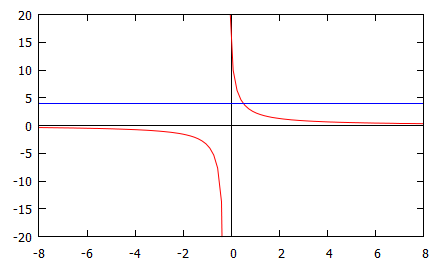
This shows the graph of $f(x)=\dfrac{14}{1+5x}$, in red, and the line $g(x)=4$ in blue. We are looking for values of $x$ for which the red line is greater than the blue line.

When looking to solve this inequality, the obvious first step would be to multiply by $1+5x$. However, this could be either positive or negative depending on the value of $x$; recall that when we multiply by a negative number, the inequality sign changes. So we must consider two cases separately:

Case 1: $1+5x \lt 0$

Case 2: $1+5x \gt 0$

First, look at Case 1.

Solve for $x$. \begin{align} 1+5x &\lt 0\\ 5x &\lt -1\\ x &\lt -\frac{1}{5} \end{align}

Now look at the whole inequality. \[\frac{14}{1+5x} \gt 4\] Multiply through by $1+5x$, remembering that we are treating it as negative so the inequality symbol changes. \[14 \lt 4(1+5x)\] Expand the brackets and simplify. \[14 \lt 4+20x\] \[10\lt 20x\] Solve for $x$. \[x\gt \frac{10}{20}=\frac{1}{2}\] We cannot have $x\lt -\dfrac{1}{5}$ and $x\gt\dfrac{1}{2}$ at the same time, so we cannot have $1+5x \lt 0$.

Now consider Case 2.

Solve for $x$. \begin{align} 1+5x &\gt 0\\ 5x &\gt -1\\ x&\gt -\frac{1}{5} \end{align}

Now look at the whole inequality. \[\frac{14}{1+5x} \gt 4\] Multiply through by $1+5x$. This time we are treating it as positive so the inequality symbol will remain the same. \[14 \gt 4(1+5x)\]

Expand and simplify.

\begin{align} 14 &\gt 4+20x \\ 10 &\gt 20x \end{align}

Solve for $x$.

\[x\lt \frac{10}{20}=\frac{1}{2}\]

Combining the two inequalities we have derived for $x$, the solutions are given by $-\dfrac{1}{5} \lt x \lt \dfrac{1}{2}$.

In set notation, this is \[\left(-\dfrac{1}{5},\dfrac{1}{2}\right).\]