Limits of Functions
Definition
A limit is the (output) value that a function or sequence approaches as the input approaches some particular value. The notation for limits is
\[\displaystyle{\lim_{x\rightarrow c} f(x) = l}\]
which means: the limit of the function $f(x)$ as $x$ tends to $c$ is $l$.
One Sided Limits
Alternatively, $x$ may approach $c$ from above (right) or below (left), in which case the limits may be written as: \[\displaystyle{\lim_{x\to c^+} f(x) = l} \;\text { or }\;\displaystyle{\lim_{x\to c^-} f(x) = l}\]
respectively.
If both of these limits are equal to $l$, then this can be referred to as the limit of $f(x)$ at $c$. Conversely, if they are both not equal to $l$, then the limit does not exist.
Properties
Properties of limits as $x$ approaches some value $c$.
- $\displaystyle{\lim_{x\to c} \bigl(f(x)+g(x)\bigr) = \lim_{x\to c} f(x) +\lim_{x\to c} g(x)}$
- $\displaystyle{\lim_{x\to c} \bigl(f(x)-g(x)\bigr) = \lim_{x\to c} f(x) -\lim_{x\to c} g(x)}$
- $\displaystyle{\lim_{x\to c} \bigl(f(x) \times g(x)\bigr) = \lim_{x\to c} f(x) \times \lim_{x\to c} g(x)}$
- $\displaystyle{\lim_{x\to c} \left(\frac{f(x)}{g(x)}\right) = \frac{\lim_{x\to c} f(x)}{\lim_{x\to c} g(x)}}$
As $x\rightarrow\infty$
The function $f(x) \rightarrow l$, a real limit, as $x\rightarrow\infty$ if, however small a distance we choose, $f(x)$ gets closer than this distance to $l$.
The function $f(x)\rightarrow \infty$ as $x\rightarrow\infty$ if, however large a number we choose, $f(x)$ gets larger than this number.
The function $f(x) \rightarrow -\infty$ as $x\rightarrow\infty$ if, however large and negative a number we choose, $f(x)$ gets more negative than this number.
As $x\rightarrow -\infty$
The function $f(x) \rightarrow l$, a real limit, as $x\rightarrow -\infty$ if, however small a distance we choose, $f(x)$ gets closer than this distance to $l$.
The function $f(x)\rightarrow \infty$ as $x\rightarrow -\infty$ if, however large a number we choose, $f(x)$ gets larger than this number.
The function $f(x) \rightarrow -\infty$ as $x\rightarrow -\infty$ if, however large and negative a number we choose, $f(x)$ gets more negative than this number.
As $x\rightarrow c$
The limit of $f(x)$ as $x$ tends to a real number $c$, is the value $f(x)$ approaches as $x$ gets closer to that real number.
Common Limits
Whilst it is necessary to know how to work out all limits, it is useful to know some that appear often.
- $\displaystyle{\lim_{x\to c} a = a}$
- $\displaystyle{\lim_{x\to c} x^r = c^r}$ for $r \geq 1$
- $\displaystyle{\lim_{x\to 0^+} \frac{1}{x^r} = \infty}$
- $\displaystyle{\lim_{x\to 0^-} \frac{1}{x^r} =
\begin{cases} -\infty, \;\;\text{if } r \text{ is odd}\\ +\infty, \;\;\text{if } r \text{ is even}
\end{cases}}$
- $\displaystyle{\lim_{x\to \infty} x^N =
\begin{cases} \begin{align} \infty, \;\;&N\gt 0\\ 1, \;\; &N=0\\ 0, \;\;&N\lt 0 \end{align} \end{cases}}$
- $\displaystyle{\lim_{x\to \infty} N^x =
\begin{cases} \begin{align} \infty, \;\;&N\gt 1\\ 1, \;\; &N=1\\ 0, \;\;&0\lt N \lt 1. \end{align} \end{cases}}$
- $\displaystyle{\lim_{x\to \infty} \frac{x}{N} =
\begin{cases} \begin{align} \infty, \;\;&N\gt 0\\ \text{does not exist}, \;\; &N=0\\ -\infty, \;\;&N\lt 0 \end{align} \end{cases}}$
- $\displaystyle{\lim_{x\to \infty} \frac{N}{x} = 0}$ for any real $N$
Worked Examples
Example 1
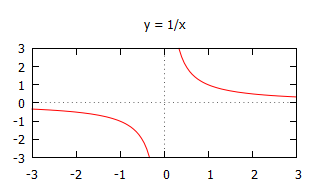
Find the limit of the function $f(x) = \dfrac{1}{x}$ as $x\rightarrow\infty$.
Solution
To start, put a few increasing values of $x$ into the function to get an idea of the behaviour of $f(x)$. It may also be helpful to look at the graph of $f(x) = \dfrac{1}{x}$.
|
$x$ |
1 |
2 |
3 |
4 |
10 |
20 |
100 |
|---|---|---|---|---|---|---|---|
|
$f(x)$ |
1 |
$\dfrac{1}{2}$ |
$\dfrac{1}{3}$ |
$\dfrac{1}{4}$ |
$\dfrac{1}{10}$ |
$\dfrac{1}{20}$ |
$\dfrac{1}{100}$ |
We can see that as the values of $x$ increase, the value of $f(x)$ is getting closer to zero, and we know the function $\dfrac{1}{x}$ can never be equal to zero.
So we say $f(x) \rightarrow 0$ as $x\rightarrow\infty$ or $\displaystyle{\lim_{x\rightarrow\infty} \frac{1}{x}~} = 0$.
Example 2
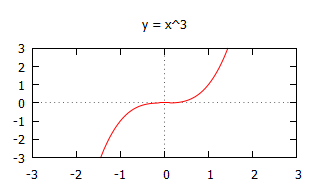
Find the limit of the function $f(x) = x^3$ as $x\rightarrow -\infty$.
Solution
To start, put a few decreasing values of $x$ into the function to get an idea of the behaviour of $f(x)$. It may also be helpful to look at the graph of $f(x) = x^3$.
|
$x$ |
0 |
-1 |
-2 |
-3 |
-10 |
-20 |
-100 |
|---|---|---|---|---|---|---|---|
|
$f(x)$ |
0 |
-1 |
-8 |
-27 |
-1000 |
-8000 |
-1000000 |
We can see that as the values of $x$ decrease, the value of $f(x)$ is clearly getting more and more negative.
So we say $f(x) \rightarrow -\infty$ as $x\rightarrow -\infty$ or $\displaystyle{\lim_{x\rightarrow -\infty} x^3} = -\infty$.
Example 3
Find the limit of the function $f(x) = x+4$ as $x\rightarrow 1$.
Solution
As the function exists at $x=1$, we can just put this value into the function and find a value for $f(x)$.
So we have that $f(x) \rightarrow 5$ as $x\rightarrow 1$ or $\displaystyle{\lim_{x\rightarrow 1} (x+4)} = 5$.
Video Examples
Example 1
Prof. Robin Johnson finds the limit of $\dfrac{x^2+1}{x^3+1}$ as $x\rightarrow 1$.
Example 2
Prof. Robin Johnson finds the limit of $\dfrac{x^2-4}{x-2}$ as $x\rightarrow 2$.
Example 3
Prof. Robin Johnson finds the limit of $\dfrac{\sin 3x}{\tan x}$ as $x\rightarrow 0$.
External Resources
- Limits of functions workbook at mathcentre.