The Sine and Cosine Rules
Definition
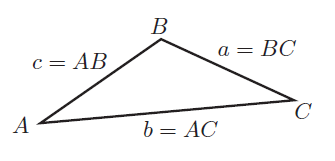
The sine and cosine rules can be used on any triangle. In the diagram below, the sides are labelled lower case $a$, $b$ and $c$ and the corresponding angles opposite the sides are labelled upper case $A$, $B$ and $C$.
|center
The sine rule is \[\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\] This is used when given two angles and one side, or two sides and a non-included angle.
The cosine rule is \[a^2 = b^2 + c^2 - 2bc\cos A\text{.}\] This is used when given all three sides, or two sides and the angle in-between.
Worked Examples
In the examples below, $a$, $b$ and $c$ refer to lengths of sides and $A$, $B$ and $C$ refer to the corresponding opposite angles.
Example 1
Given $a=3$, $b=4$, $A=40^{\circ}$, find $B$.
Solution
Use the sine rule $\dfrac{a}{\sin A} = \dfrac{b}{\sin B}$ to find $B$.
Substitute the given values of $a$, $A$ and $b$. \[\frac{3}{\sin 40^{\circ} } = \frac{4}{\sin B}\] Multiply both sides by $\sin B$ and $\sin 40^{\circ}$. \begin{align} 3\sin B &= 4 \sin 40^{\circ}\\\\ \sin B &= \frac{4 \sin 40^{\circ} }{3}\\ B &= \sin^{-1} \left(\frac{4 \sin 40^{\circ} }{3}\right)\\ B &= 58.99^{\circ} \text{ (to 2 d.p.)} \end{align}
Example 2
Given $b=6$, $B=77^{\circ}$ and $C=34^{\circ}$, find $c$. Also find $a$ and $A$.
Solution
First, use $\dfrac{b}{\sin B} = \dfrac{c}{\sin C}$ to find $c$.
\begin{align} \frac{6}{\sin 77^{\circ} } &= \frac{c}{\sin 34^{\circ} }\\\\ \frac{6 \sin 34^{\circ} }{\sin 77^{\circ} } &= c\\ c &= 3.44 \text{ (to 3 sig.fig.)} \end{align}
To find $A$, use the fact that the angles in a triangle add up to $180^{\circ}$, i.e. $A+B+C = 180$.
\begin{align} 180 &= A +77 + 34\\ A &= 180 - 77- 34\\ A &= 69^{\circ} \end{align}
Now, use this value for $A$ in the sine rule to find $a$.
\begin{align} \frac{a}{\sin 69^{\circ} } &= \frac{6}{\sin 77^{\circ} }\\\\ a &= \frac{6 \sin 69^{\circ} }{\sin 77^{\circ} }\\\\ a &= 5.75 \text{ (to 3 sig.fig.)} \end{align}
Example 3
Given $b=2$, $c=5$ and $A=39^{\circ}$, find $a$.
Solution
Use $a^2 = b^2 + c^2 -2bc\cos A$.
\begin{align} a^2 &= 2^2 + 5^2 - (2\times2\times5)\cos 39^{\circ}\\ a^2 &= 29 - 20\cos 39^{\circ}\\ a^2 &= 13.457 \text{ (to 3 d.p.)}\\ a &= 3.67 \text{ (to 3 sig.fig.)} \end{align}
Example 4
Given $a=7$, $b=6$ and $c=9$. Find the angle between $a$ and $b$.
Solution
The angle between $a$ and $b$ is labelled $C$ in the diagram above, so use $c^2 = a^2 + b^2 - 2ab\cos C$.
\begin{align} 9^2 &= 7^2 + 6^2 - (2\times7\times6)\cos C\\ 81 &= 49+36 - 84\cos C\\ 84\cos C &= 4\\ \cos C &= \frac{4}{84} = \frac{1}{21}\\\\ C &= \cos^{-1}\left(\frac{1}{21}\right)\\ C &= 87.3^{\circ} \text{ (to 3 sig.fig.)} \end{align}
Workbook
This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.
Applications of trigonometry to triangles contains examples on the sine and cosine rule.
External Resources
- Triangle formulae workbook at mathcentre.