Numeracy, Maths and Statistics - Academic Skills Kit

Vectors in Cartesian Coordinates

ContentsToggle Main Menu 1 Definition and Notation 2 Properties2.1 Addition and Subtraction2.2 Scalar Multiplication2.3 Length 3 Unit Vectors 4 Worked Example 5 Workbooks 6 See Also 7 External Resources

Definition and Notation

A vector is a geometric object which has both magnitude (size) and direction.

Vectors are typically denoted in print as lowercase letters in boldface.

Example: $\boldsymbol{\mathrm{a} }$.

In handwriting, a tilde, arrow or underline is used to denote a vector. The convention for handwritten notation varies with geography and subject area.

Example: $\tilde{a}$, $\vec{a}$, $\underline{a}$, $\underset{^\sim}a$

Vectors can be described using Cartesian coordinates, giving the components of the vector along each of the axes.

Example: $ \boldsymbol{\mathrm{a} }=(a_1,a_2,a_3) $.

$\boldsymbol{\mathrm{e} }_1=(1,0,0)$ is a vector of length 1 in the $x$ direction, $\boldsymbol{\mathrm{e} }_2=(0,1,0)$ is a vector of length 1 in the $y$ direction and $\boldsymbol{\mathrm{e} }_3=(0,0,1)$ is a vector of length 1 in the $z$ direction. The notations $\hat{\boldsymbol{\mathrm{e} } }_1,\hat{\boldsymbol{\mathrm{e} } }_2,\hat{\boldsymbol{\mathrm{e} } }_3$; $\boldsymbol{\mathrm{i} },\boldsymbol{\mathrm{j} },\boldsymbol{\mathrm{k} }$; and $\hat{\boldsymbol{\mathrm{x} } },\hat{\boldsymbol{\mathrm{y} } },\hat{\boldsymbol{\mathrm{z} } }$ are equivalent to $\boldsymbol{\mathrm{e}_1},\boldsymbol{\mathrm{e}_2},\boldsymbol{\mathrm{e}_3}$.

A vector can also be described as a sum of multiples of each of the unit basis vectors.

Example: $\boldsymbol{\mathrm{a} }=a_1\boldsymbol{\mathrm{e} }_1+a_2\boldsymbol{\mathrm{e} }_2+a_3\boldsymbol{\mathrm{e} }_3$.

Example

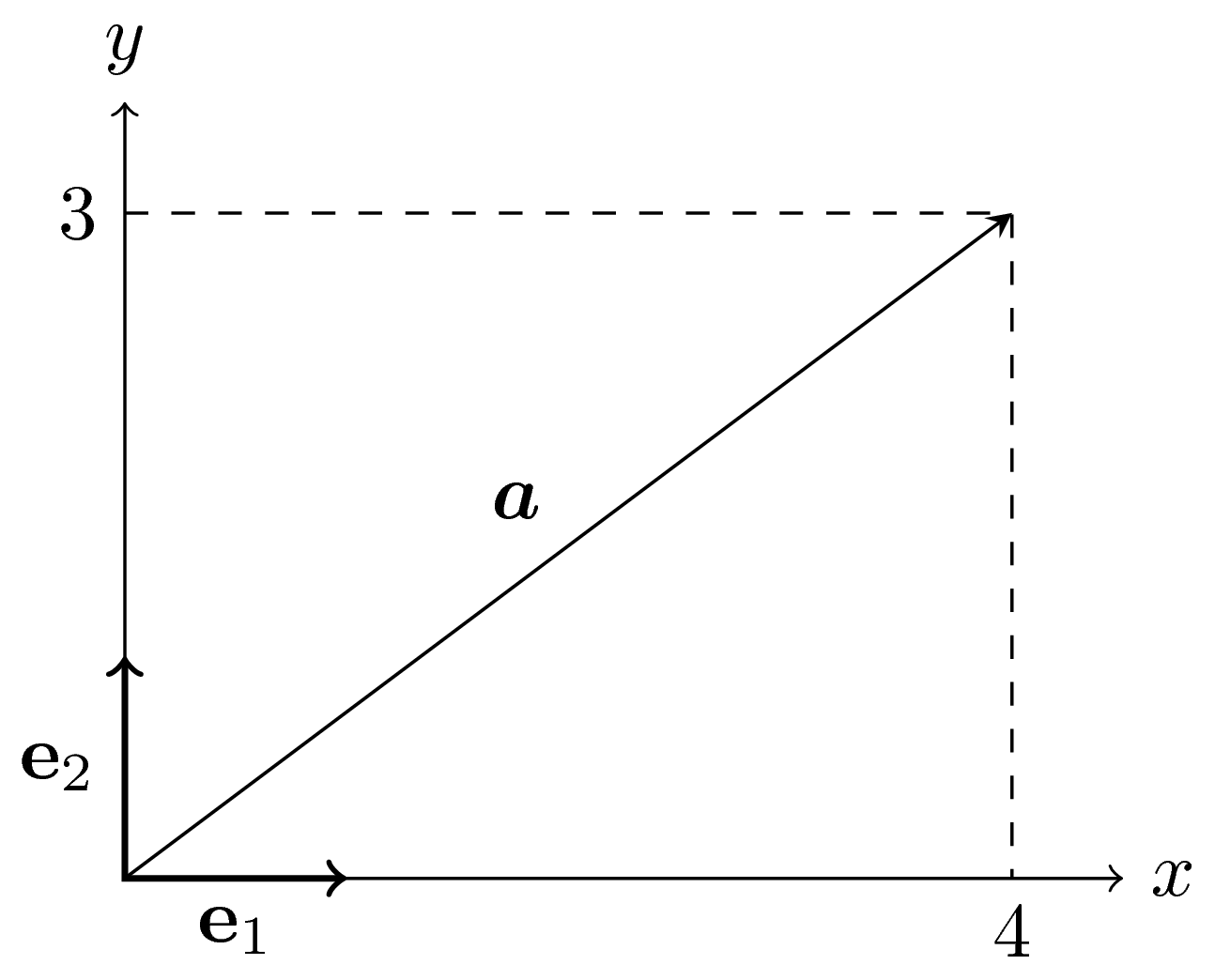
|440px|center

A two-dimensional vector $\boldsymbol{\mathrm{a}}=(4,3)=4\boldsymbol{\mathrm e}_1+3\boldsymbol{\mathrm e}_2$.

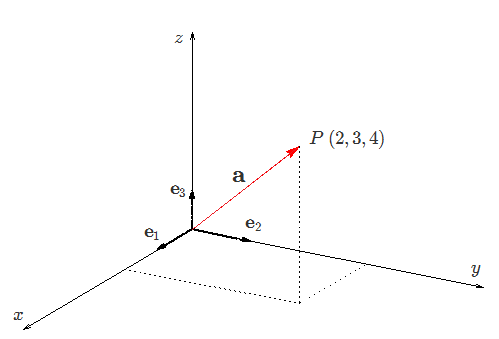
| 500px | center

A three-dimensional vector $\boldsymbol{\mathrm{a}}$, beginning at the origin and ending at the point $P(2,3,4)$. The vector $\boldsymbol{\mathrm{a}}$ can be expressed in the following ways:

$\boldsymbol{\mathrm{a}}=(2,3,4)$
$\boldsymbol{\mathrm{a}}=2\boldsymbol{\mathrm e}_1+3\boldsymbol{\mathrm e}_2+4\boldsymbol{\mathrm e}_3$

Properties

Addition and Subtraction

Addition and subtraction in vectors works component-wise.

Given vectors $\boldsymbol{\mathrm{a} }=(a_1,a_2,a_3)$ and $\boldsymbol{\mathrm{b} }=(b_1,b_2,b_3)$ the following properties hold:

$\displaystyle{ \boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }=(a_1+b_1,a_2+b_2,a_3+b_3) } $
$\displaystyle{ \boldsymbol{\mathrm{a} }-\boldsymbol{\mathrm{b} }=(a_1-b_1,a_2-b_2,a_3-b_3). } $

Or, equivalently:

$\displaystyle{ \boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }=(a_1+b_1){\boldsymbol{\mathrm{e} }_1}+(a_2+b_2){\boldsymbol{\mathrm{e} }_2}+(a_3+b_3){\boldsymbol{\mathrm{e} }_3} }$
$\displaystyle{ \boldsymbol{\mathrm{a} }-\boldsymbol{\mathrm{b} }=(a_1-b_1){\boldsymbol{\mathrm{e} }_1}+(a_2-b_2){\boldsymbol{\mathrm{e} }_2}+(a_3-b_3){\boldsymbol{\mathrm{e} }_3}. }$

Scalar Multiplication

Given a vector $\boldsymbol{\mathrm{a} }=(a_1,a_2,a_3)$ and a scalar (real number) $\lambda$ the following property holds:

\[\displaystyle{ \lambda\boldsymbol{\mathrm{a} }=(\lambda a_1,\lambda a_2,\lambda a_3). }\]

Or, equivalently

\[\displaystyle{ \lambda\boldsymbol{\mathrm{a} }=\lambda a_1\boldsymbol{\mathrm{e} }_1 + \lambda a_2\boldsymbol{\mathrm{e} }_2 + \lambda a_3\boldsymbol{\mathrm{e} }_3. }\]

Properties of Scalar Multiplication

For any vectors $\boldsymbol{\mathrm{a} },\boldsymbol{\mathrm{b} }$ and scalars $\lambda,\mu$ the following properties hold:

Distributivity
- $\lambda(\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} })=\lambda\boldsymbol{\mathrm{a} } + \lambda\boldsymbol{\mathrm{b} }$
- $(\lambda+\mu)\boldsymbol{\mathrm{a} }=\lambda\boldsymbol{\mathrm{a} }+\mu\boldsymbol{\mathrm{a} }$

Associativity
- $(\lambda\mu)\boldsymbol{\mathrm{a} }=\lambda(\mu\boldsymbol{\mathrm{a} })$

Length

The length of a vector $\boldsymbol{\mathrm{a} }=(a_1,a_2,a_3)$ is denoted $\lvert\boldsymbol{\mathrm{a} }\rvert$ or $\lVert \boldsymbol{\mathrm{a} }\rVert$ and can be calculated in the following way:

\[\lvert\boldsymbol{\mathrm{a} }\rvert=\sqrt{a_1^2+a_2^2+a_3^2}\]

The length of a vector is also referred to as its magnitude or norm.

Unit Vectors

A unit vector is a vector of length $1$. A “hat” is typically used to denote that a vector is a unit vector.

Example: A vector of length 1 in the direction of vector $\boldsymbol{\mathrm{a} }$ is denoted $\hat{\boldsymbol{\mathrm{a} } }$.

A non-zero vector $\boldsymbol{\mathrm{a} }$ can be scaled by the reciprocal of its length to obtain the unit vector $\hat{\boldsymbol{\mathrm{a} } }$. This process is known as normalising a vector.

\[\hat{\boldsymbol{\mathrm{a} } }=\cfrac{\boldsymbol{\mathrm{a} } }{\lvert\boldsymbol{\mathrm{a} }\rvert}=\left(\cfrac{a_1}{\lvert\boldsymbol{\mathrm{a} }\rvert},\cfrac{a_2}{\lvert\boldsymbol{\mathrm{a} }\rvert},\cfrac{a_3}{\lvert\boldsymbol{\mathrm{a} }\rvert}\right)\]

Worked Example

Example 1

Given vectors $\boldsymbol{\mathrm{a} }=\left(4,-3,9\right)$ and $\boldsymbol{\mathrm{b} }=(7,5,-2)$, find the unit vector in the direction of $\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }$.

Solution

By the properties of addition and subtraction, the $i$^th component of $\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }$ is the sum of the $i$^th component of $\boldsymbol{\mathrm{a} }$ and the $i$^th component of $\boldsymbol{\mathrm{b} }$. For example, the first component of $\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }$ is $4+7=11$.

Thus, \begin{align} \boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} } &= \left(4+7,\,-3+5,\,9-2\right) \\ &=\left(11,\,2,\,7\right). \end{align}

Recall that the unit vector in the direction of a vector $\boldsymbol{\mathrm{x} }$ is given by

\[\hat{\boldsymbol{\mathrm{x} } }=\dfrac{\boldsymbol{\mathrm{x} } }{\lvert\boldsymbol{\mathrm{x} }\rvert}.\]

Therefore the length of the vector $\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }$ must be calculated:

\begin{align} \lvert\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }\rvert &= \sqrt{\strut{11^2+2^2+7^2} } \\ &=\sqrt{174}. \end{align}

It is generally preferred to leave this quantity in surd form, rather than calculate a decimal approximation.

Hence, the unit vector in the direction of $\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} }$ is

\begin{align} \widehat{\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} } } &= \dfrac{1}{\sqrt{174} }\left(11,2,7\right) \\ &= \left(\dfrac{11}{\sqrt{174} },\dfrac{2}{\sqrt{174} },\dfrac{7}{\sqrt{174} }\right). \end{align}

Or, equivalently,

\[\widehat{\boldsymbol{\mathrm{a} }+\boldsymbol{\mathrm{b} } }=\dfrac{11}{\sqrt{174} }\boldsymbol{\mathrm{e} }_1+\dfrac{2}{\sqrt{174} }\boldsymbol{\mathrm{e} }_2+\dfrac{7}{\sqrt{174} }\boldsymbol{\mathrm{e} }_3.\]

Workbooks

These workbooks produced by HELM are good revision aids, containing key points for revision and many worked examples.

External Resources

Introduction to vectors workbook at mathcentre.
Cartesian components of vectors workbook at mathcentre.
Introduction to vectors videos at Khan Academy.