Net Present Value and Internal Rate of Return (Finance)
Net Present Value
The value of the net cash flow at time $t=0$ is called the net present value. In order to get the net present value, one must discount each payment back to time $0$ and then sum them all.
Suppose you gain $x_1$ at time $1$, $x_2$ at time $2$ and so on up to $x_n$ at time n. Then the NPV is given by: \[\text{NPV }=x_1 v^1+x_2 v^2+x_3 v^3+\ldots+x_n v^n\] Recall that $v=\frac{1}{1+i}$.
Worked Example 1
Worked Example
Suppose a builder buys a plot of land at time $0$ for $£50,000$. One month later, he pays wages for a total of $£60,000$. He buys other building material worth $£30,000$ three months after purchasing the land. He sells the house that he has built for $£150,000$ after one year.
What is the net present value if:
a) The interest rate is $6\%$?
b) The interest rate is $10\%$?
Solution
a) \begin{align} \text{NPV}&=-50,000-\dfrac{60,000}{(1+0.06)^{\left(\frac{1}{12}\right)}~} -\frac{30,000}{(1+0.06)^{0.25}~} +\frac{150,000}{(1+0.06)},\\ &\approx£2,233.92. \end{align}
b) \begin{align} \text{NPV}&= -50,000-\frac{60,000}{(1+0.1)^{\left(\frac{1}{12}\right)}~} -\frac{30,000}{(1+0.1)^{0.25}~} +\frac{150,000}{(1+0.1)}, \\ &\approx-£2,455.32. \end{align}
Internal Rate of Return
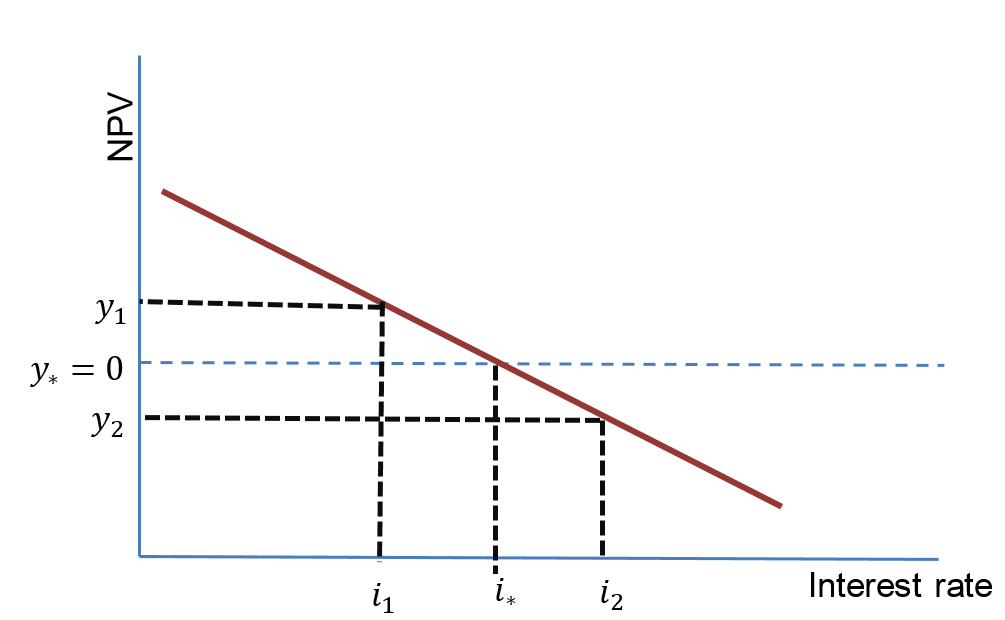
The internal rate of return (or the yield) is the interest rate at which the net present value is equal to zero i.e. NPV$(i)=0$.
The IRR can be positive, negative and sometime there may be no solution, a unique solution or there can be multiple solutions.
In order to approximate the net present value, one can use linear interpolation. To use this you must have a positive net present value -and the interest that gives this value- and a negative net present value along with the corresponding interest rate.
To approximate the IRR, one can use the following formula: \[i_{*}=i_1+\frac{i_2-i_1}{y_2-y_1}(y_{*}-y_1)\] where:
- $i_{*}=$ the interest rate which gives an NPV of zero
- $i_1=$ the interest rate that gives a positive NPV
- $i_2=$ the interest rate that gives a negative NPV
- $y_1=$ positive NPV
- $y_2=$ negative NPV
- $y_{*}=0$
Worked Example 2
Worked Example
Using the example above, approximate the internal rate of return using linear interpolation.
Solution
\begin{align} \text{NPV }(6\%)&=£2,233.92\\ \text{NPV}(10\%)&=-£2,455.32\\ i_{*}&=0.06+\frac{0.1-0.06}{-2455.32-2233.92}(0-2233.92)\\ \Rightarrow i_{*}&=0.07905571052\\ \Rightarrow i_{*}&\approx7.91\%. \end{align}
Video Example
Dr Graham Murphy solving a net present value and internal rate of return problem.