Impulse and Momentum (Mechanics)
Momentum and Impulse
The momentum, $p$, of a body of mass $m$ which is moving with a velocity $v$ is $p = m \times v = mv$. The units are $\mathrm{Ns}$.
The impulse of a force is $I = Ft$ - when a constant force $F$ acts for a time $t$. The units are $\mathrm{Ns}$.
The Impulse-Momentum Principle says $I = mv - mu$ which is final momentum - initial momentum so Impulse is the change in momentum.
The principle of states that total momentum before impact is equal to total momentum after impact, $m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2.$
\begin{align*} p &= mv,\\ I & = Ft, \\ I & = mv - mu, \\ m_1 u_1 + m_2 u_2 & = m_1 v_1 + m_2 v_2. \end{align*}
Worked Example: Impulse-Momentum Principle
Finding the magnitude of the Impulse
A ball of mass $400\mathrm{g}$ hits a fixed vertical wall at a right angle with a speed of $5 \mathrm{ms^{-1} }$, the ball rebounds with a speed of $3 \mathrm{ms^{-1} }$. What is the impulse exerted on the wall by the ball?
Solution
We can find the impulse exerted on the ball by the wall and then use 's 3rd Law (every action has an equal and opposite reaction) to deduce the impulse exerted on the wall by the ball - as these will be equal.
If we take the rebound direction of the ball as the positive direction, and convert the mass of the ball to $\mathrm{kg}$, we have that \begin{align} I & = mv - mu, \\ & = \left(0.4 \times 3 \right) - \left(0.4 \times (-5) \right), \\ & = 1.2 - (-2), \\ & = 3.2 \mathrm{N s}. \end{align} Note that the initial velocity is in the negative direction. So therefore by 's 3rd Law, the magnitude of the impulse exerted on the wall by the ball is $3.2 \mathrm{Ns}$.
Worked Example: Principle of Momentum Conservation
Finding speed and direction of two colliding particles
Two particles $P$ and $Q$ of mass $5 \mathrm{kg}$ and $8\mathrm{kg}$ respectively are moving towards each other along the same straight line. The surface is smooth and horizontal and the particles move at speeds $4 \mathrm{ms^{-1} }$ and $2 \mathrm{ms^{-1} }$ respectively. $P$ and $Q$ collide. The magnitude of the impulse due to the collision is $8 \mathrm{Ns}$. What is the speed and direction of each particle after the collision?
Solution
First draw a diagram which shows the velocities and impulses with arrows.
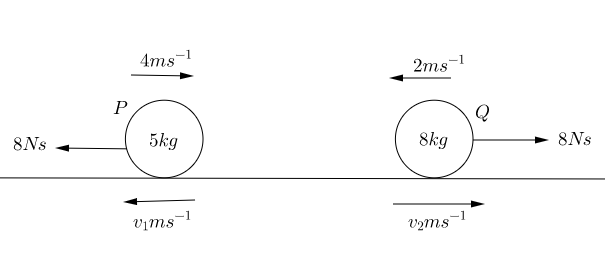
Here we have guessed that the particles will change direction on collision - they may not! To find the velocities after collision we consider each particle one at a time, choose a positive direction and apply the Impulse-Momentum Principle.
For particle $P$ we will take the direction $\left( \leftarrow \right)$ as the positive. \begin{align} I & = mv - mu,\\ 8 & = 5(v_1 - (-4)), \\ 8 & = 5v_1 + 20, \\ - 12 & = 5 v_1, \\ -2.4 \mathrm{ms^{-1} } & = v_1, \end{align} We have that $v_1 < 0$ this means our guess for the direction of $P$ was incorrect - this is okay, it just means that after the collision $P$ was travelling in the direction $(\rightarrow)$ at a speed of $2.4 \mathrm{ms^{-1} }$ so it doesn't change direction.
For particle $Q$ we will take the direction $\left(\rightarrow \right)$ as the positive. \begin{align} I & = mv - mu,\\ 8 & = 8(v_2 - (-2)), \\ 8 & = 8v_2 +16, \\ -8 & = 8 v_2, \\ -1 \mathrm{ms^{-1} } & = v_2. \end{align} We have that $v_2 <0$ this means our guess for the direction of $Q$ was also incorrect - this is okay, it means that after the collision $Q$ didn't change direction either, and was travelling in the direction $\left( \leftarrow \right)$ at a speed of $1 \mathrm{ms^{-1} }$.
Test Yourself
Try our Numbas test on impulse and momentum: Impulse and Momentum