Moments (Mechanics)
Moments
The turning effect of the force on the body on which it is acting is measured by the moment of a force.
The moment of a force depends on the magnitude of the force and the distance from the axis of rotation.
The moment of a force about a point is (the magnitude of the force) $\times$ (the perpendicular distance of the line of action of the force from the point).
When there are several forces acting on a body the moments about a point can be added so long as a positive direction (clockwise or anticlockwise) is specified and is considered for each moment.
Worked Example: Finding the moment
Find the moment of $F$ about $P$
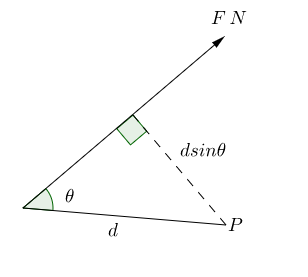
Find the moment of $F$ about $P$ in the above diagram. Find the moment of $F$ about $P$ when $\theta = 35^{\circ}, F = 8$ and $d = 14$.
Solution
Moment of $F$ about $P$ is $F \times d sin \theta$ clockwise. Here, we have found the perpendicular distance from $P$ using trigonometry and multiplied it by the magnitude of the force. When describing a moment you need to give a direction of rotation. Therefore when we are given the values this is \begin{align} \text{Moment} & = F \times d \sin \theta, \\ & = 8 \times 14\sin(35^{\circ}), \\ &= 64.241\mathrm{Nm} \text{ (to 3d.p.).} \end{align} The moment of the force is measured in newton-metres $\mathrm{N m}$, therefore the moment of $F$ about $P$ is $64.241\mathrm{Nm}$.
Sum of moments
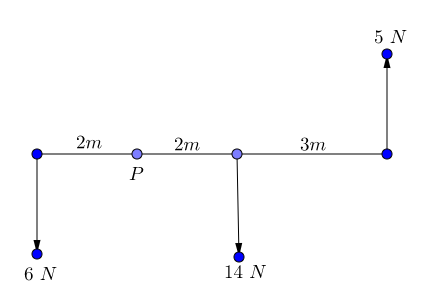
The diagram shows a set of forces acting on a light rod. Calculate the sum of the moments about the point $P$.
Solution
Each force is already perpendicular to the point $P$.
The moment of the $6\mathrm{N}$ force is $6 \times 2 = 12 \mathrm{N m}$ anticlockwise.
The moment of the $14\mathrm{N}$ force is $14 \times 2 = 28 \mathrm{N m}$ clockwise.
The moment of the $5\mathrm{N}$ force is $5 \times (2+3) = 25 \mathrm{Nm}$ anticlockwise.
Total clockwise $= 28 \mathrm{N m}$ and total anticlockwise $= 37 \mathrm{Nm}$. Therefore the sum of the moments is $37 - 28 = 9 \mathrm{Nm}$ anticlockwise. As the anticlockwise total was greater we chose anticlockwise as the positive direction.
Worked Example: Finding the moment when the distance given is not perpendicular
Find the moment of the force about $P$
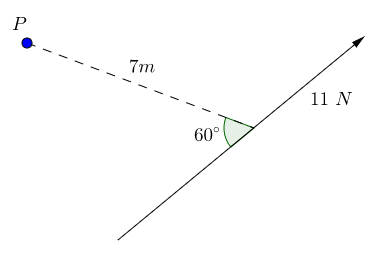
Find the moment of the force about $P$ in the above diagram.
Solution
The perpendicular distance from $P$ to the force will be the distance opposite the angle given by $7 \sin (60^{\circ})$. Therefore \begin{align} \text{The moment of the force} & = 11 \times 7 \sin (60^{\circ}), \\ & = 77 \sin (60^{\circ}), \\ & = 66.684 \mathrm{Nm} \text{ anticlockwise (3 d.p.).} \end{align}
Worked Example: Bodies resting in equilibrium
Finding the normal reactions
Suppose that there is a uniform rod of length $9\mathrm{m}$ and weight $30\mathrm{N}$. It rests on a support $X$ at one end point and a support $Y$ which is $5\mathrm{m}$ away from support $X$. Calculate the magnitude of the reaction at each of the supports.
Solution
We can draw a diagram showing all the forces acting.
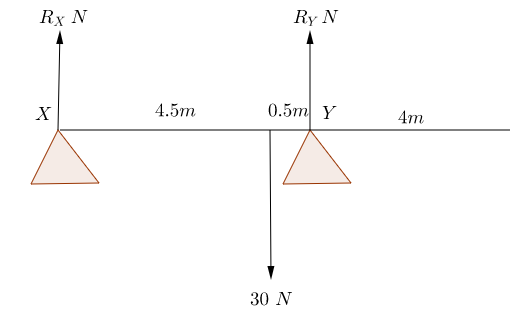
The weight of the rod will act at its centre of mass - as it is a uniform rod the weight acts at the mid-point. The rod is in equilibrium so the total forces acting upwards will equal the total forces acting downwards when we resolve vertically. \begin{equation} R_X + R_Y = 30. \end{equation} Consider the moments about point $X$, we have that clockwise moments will equal anticlockwise moments therefore \begin{align} 30 \times 4.5 & = R_Y \times (4.5 + 0.5), \\ 135 & = 5R_Y, \\ 27 \mathrm{N} & = R_Y. \end{align} Now we can use this value to find $R_X$ \begin{align} R_X + R_Y & = 30, \\ R _ X & = 30 - 27, \\ & = 3 \mathrm{N}. \end{align} Therefore the reaction at point $X$ is $3 \mathrm{N}$ and the reaction at point $Y$ is $27\mathrm{N}$.
Finding the centre of mass in a non-uniform body
Suppose that there is a non-uniform rod $AB$ of length $10\mathrm{m}$ and weight $15\mathrm{N}$. It is in a horizontal position and rests on supports at points $C$ and $D$. The distance $A C = 3m$ and $AD = 7m$. The magnitude of the reaction at $C$ is four times the magnitude of the reaction at $D$. Find the distance of the centre of mass of the rod from $A$.
Solution
We can draw a diagram showing all the forces acting.
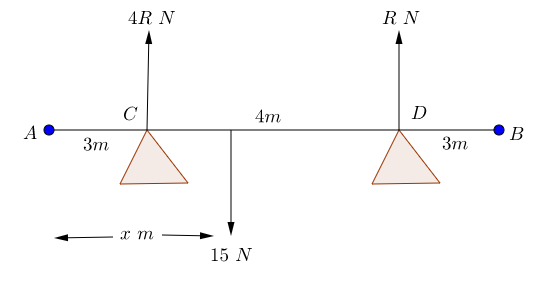
Here we have assumed that the centre of mass acts at a point $x$ m from point $A$. As the rod is not uniform we can not say that the centre of mass is at the mid point of the rod. We resolve vertically \begin{align} 4R + R & = 15, \\ 5R & = 15, \\ R & = 3. \end{align} Now we take moments about point $A$ \begin{align} 15 \times x & = (4R \times 3) + (R \times 7), \\ & = 36 + 21, \\ & = 57, \\ x & = 3.8. \end{align} The centre of mass is $3.8 \mathrm{m}$ from $A$.