The i,j notation (Mechanics)
Vector notation
Index notation for vector calculus involves basis vectors $\underline{e}_x$ and $\underline{e}_y$ for two dimensions.
In the examples that follow in Mechanics however we will be using $i,j$ notation.
The $i,j$ notation
A vector can be described using $\mathbf{i, j}$ notation.
A unit vector is a vector of length 1, in Cartesian co-ordinates the unit vectors along the axis are denoted by $\mathbf{i}$ and $\mathbf{j}$ respectively.
Any two-dimensional vector can be written in the form $a\mathbf{i} + b\mathbf{j}$.
Worked Example: Representing vectors
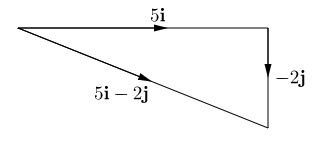
Draw a diagram
Draw a diagram to represent the vector $5\mathbf{i} - 2\mathbf{j}$.
Solution
We take 5 units in the direction of the unit vector $\mathbf{i}$ and 2 units in the direction of the unit vector $-\mathbf{j}$.
Worked Example: Problems with vectors
Problems
Given that $\mathbf{x} = 8\mathbf{i} + 4\mathbf{j}$ and $\mathbf{y} = 12\mathbf{i} - 3\mathbf{j}$, find $\mathbf{x}+\mathbf{y}$, $\mathbf{y}-\mathbf{x}$, $3\mathbf{x}+\frac{1}{2}\mathbf{y}$, the magnitude of $\mathbf{x}$ and the angle between $\mathbf{y}$ and the positive $x$-axis.
Solution
We can add vectors by considering the $\mathbf{i}$ and $\mathbf{j}$ terms separately. \begin{align} \mathbf{x} + \mathbf{y} & = \left(8\mathbf{i} + 4\mathbf{j}\right) + \left(12\mathbf{i} - 3\mathbf{j}\right), \\ & =\left(8 \mathbf{i} + 12 \mathbf{i}\right) + \left(4 \mathbf{j} - 3\mathbf{j}\right),\\ & = 20\mathbf{i} + \mathbf{j}. \end{align} We can do the same when we subtract vectors. \begin{align} \mathbf{y} - \mathbf{x} & = \left(12\mathbf{i} - 3\mathbf{j}\right) - \left(8\mathbf{i} + 4\mathbf{j}\right), \\ & = \left(12\mathbf{i} - 8\mathbf{i}\right) + \left(- 3\mathbf{j}- 4\mathbf{j}\right), \\ & = 4\mathbf{i} - 7 \mathbf{j}. \end{align} We also have that \begin{align} 3\mathbf{x} + \frac{1}{2} \mathbf{y} & = 3 \left(8\mathbf{i} + 4\mathbf{j}\right) + \frac{1}{2} \left(12\mathbf{i} - 3\mathbf{j}\right), \\ & = \left(24\mathbf{i} + 12 \mathbf{j}\right) + \left(6\mathbf{i} - \frac{3}{2}\mathbf{j}\right), \\ & = \left( 24\mathbf{i} + 6\mathbf{i}\right) + \left(12\mathbf{j} - \frac{3}{2} \mathbf{j}\right), \\ & = 30 \mathbf{i} + \frac{21}{2}\mathbf{j}. \end{align} To find the magnitude of a vector, written $\lvert \mathbf{x} \rvert$, we can use Pythagoras' Theorem. \begin{align} \lvert \mathbf{x} \rvert & = \sqrt{8^2 + 4^2}, \\ & = \sqrt{80}, \\ & = 4\sqrt{5}, \\ & = 8.94 \text{ (3 s.f.).} \end{align} To find the angle $\theta$ between the vector $\mathbf{y} = 12\mathbf{i} - 3 \mathbf{j}$ and the positive $x$-axis we can draw a diagram to correctly identify the angle we need.
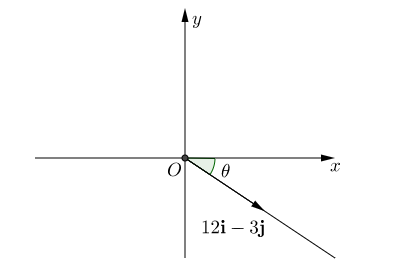
We can see that we have a right angled triangle, so can find the angle in the following way \begin{align} \tan \theta & = \frac{3}{12}, \\ \theta & = \arctan \frac{3}{12}, \\ & = 14.04^{\circ} \text{ (3 s.f.).} \end{align}