Molar Calculations

Atomic Weight

The atomic weight (or atomic mass) of an element tells us on average how much one atom of a given element weighs, taking into account typical proportions of isotopes. For example, about 98.9% of naturally occurring carbon is ¹²C ('Carbon 12') and about 1.1% is ¹³C so carbon has an atomic weight of \begin{equation} 0.989 \times 12 + 0.011 \times 13 = 12.011. \end{equation} (This type of sum is what is known as a weighted average, calculating atomic weights is actually slightly more technical than this but we won't go into the details here).

The unit for atomic weight is the Dalton (Da). Some examples of atomic weights are given below.

Element	Atomic weight (Da)
Calcium (Ca)	40.078
Carbon (C)	12.011
Hydrogen (H)	1.008
Nitrogen (N)	14.007
Oxygen (O)	15.999
Phosporus (P)	30.974
Sulphur (S)	32.066

Molecular Weight

Molecules are composed of several atoms, for example a carbon dioxide molecule (CO₂) is made up of 1 carbon atom and 2 oxygen atoms. The molecular weight (or molecular mass or relative molecular mass (RMM)) is the sum of the atomic weights of all the atoms in the molecule.

Example 1

Calculate the molecular weight of carbon dioxide - CO₂.

Solution

A molecule of carbon dioxide has 1 carbon atom and 2 oxygen atoms. Carbon has an atomic weight of 12.011 and oxygen has an atomic weight of 15.999 so the molecular weight of carbon dioxide is \begin{equation} 1 \times 12.011 + 2 \times 15.999 = 44.009 \text{ Da}. \end{equation}

Example 2

Calculate the molecular weight of monocalcium phosphate - Ca(H₂PO₄)₂.

Solution

A molecule of monocalcium phosphate has 1 calcium atom and 2 dihydrophosphate (H₂PO₄) ions. We don't need to worry too much about what an ion is here, we just note that the notation (H₂PO₄)₂ means there are 2 lots of H₂PO₄ for a total of 4 hydrogen atoms, 2 phosphorus atoms and 8 oxygen atoms. Therefore, the molecular weight of monocalcium phosphate is \begin{equation} 1 \times 40.078 + 4 \times 1.008 + 2 \times 30.974 + 8 \times 15.999 = 234.05 \text{ Da}. \end{equation}

Test yourself

Numbas test on molecular weights

Moles

A mole is the amount of a substance (in grams) that is numerically equal to its molecular weight. For example, one mole of carbon weighs 12.011 grams and one mole of monocalcium phosphate (Ca(H₂PO₄)₂) weighs 234.05 grams. The number of molecules of a substance in one mole is 6.02 $\times$ 10²³, this number is known as Avogadro's number.

If we know the molecular weight of a substance we can calculate how much a given number of moles will weigh using the formula

Example 3

Sodium chloride (NaCl) has a molecular weight of 58.44. How much does 3 moles of soduim chloride weigh?

Solution

Using the formula above, we find that 3 moles of sodium chloride weighs \begin{equation} 58.44 \times 3 = 175.32\text{g}. \end{equation} We aren't restricted to working with whole numbers for the number of moles.

Example 4

How much does 2.4 moles of calcium monophosphate (Ca(H₂PO₄)₂) weigh?

Solution

We saw in example 2 that monocalcium phosphate has a molecular weight of 234.05 so using our formula, we find that 2.4 moles of monocalcium phosphate weighs \begin{equation} 234.05 \times 2.4 = 561.72\text{g}. \end{equation}

If we know the mass of the substance and the molecular weight we can work out how many moles of the substance we have by rearranging the formula \begin{equation} \text{molecular weight} \times \text{number of moles} = \text{mass of substance} \end{equation} to get

Example 5

Glucose (C₆H₁₂O₆) has a molecular weight of 180.16, how many moles of glucose are there in 45g?

Solution

Using our rearranged formula, we find that there are \begin{equation} \frac{45}{180.16} = 0.222 \text{ moles} \end{equation} of glucose in 45g.

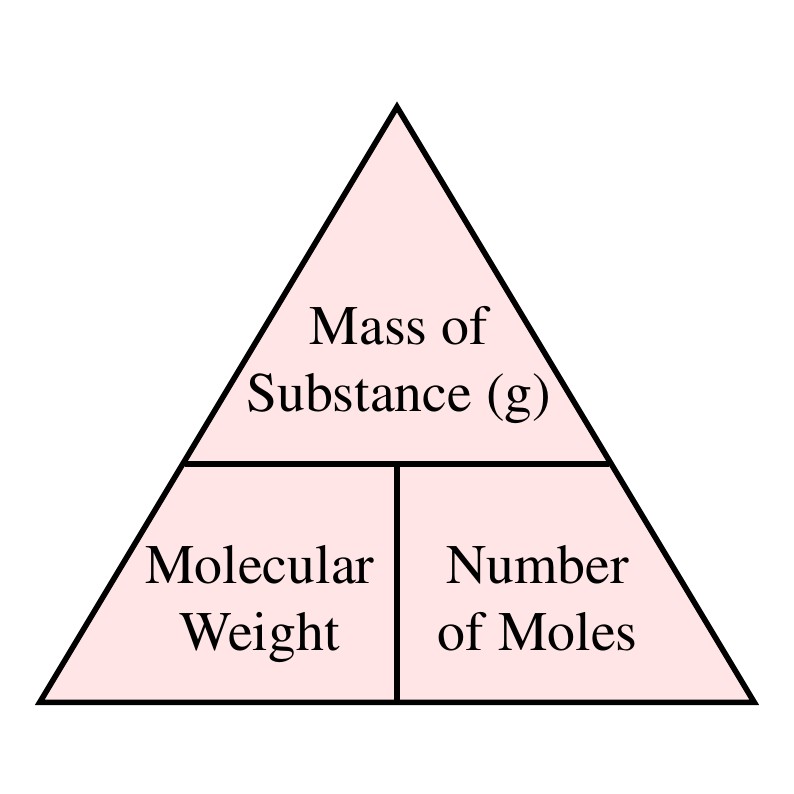
Formula Triangle

To remember the formulas in this section, you can use the formula triangle. To get the formula from the triangle, cover up the value you want to calculate and use the remaining two values. If they are next to each other, multiply them to get the answer, if one is on top of the other, divide the top one by the bottom one to get the answer.

Test yourself

Numbas test on moles

Solutions

Often, we want to dissolve a substance e.g. glucose, in a liquid e.g. water to make a solution. When we do this, we need a way to describe how much of our substance there is in a given volume of liquid, this is known as the concentration of the solution. There are different ways we can describe the concentration of a solution, we shall look at 2 of them.

1) Molarity

The molarity of a solution is equal to the number of moles of substance dissolved divided by the number of litres of solution. That is

If we have 1 mole of a substance dissolved in 1 litre of liquid (i.e. 1mol/L), we call this a 1 molar (1M) solution, if we have 1 mole of a substance dissolved in 2 litres of liquid (i.e. 0.5 mol/L), this is called a 0.5 molar (0.5M) solution and so on.

2) Mass Concentration

The mass concentration of a solution is equal to the mass of the substance dissolved divided by the volume of liquid used to make the solution. To calculate this, we use the formula

A note on units for concentrations

Sometimes, units other than g/L are used for the mass concentration, for example mg/100ml (milligrams per 100 millilitres) and there are other ways of describing the concentration other than the molarity and mass concentration. If you would like to read a little bit more about different ways of measuring the concentration of a solution see Wikipedia: Concentration. In this article, we shall just work with g/L when using the mass concentration. If you do use different units for the mass concentration be careful when using the formulas in this article. The formulas in this article use mass concentration in (g/L) so you will have to convert the units you are using to (g/L) in order to use them. For more information on how to do this, see the section on dimensions.

Let's look at some examples that deal with molarity.

Example 6

7 moles of a substance are dissolved in 4 litres of liquid to make a solution, what is the concentration of the solution in M (mol/L)?

Solution

Using our formula, we find that the concentration is \begin{equation} \frac{7}{4} = 1.75\text{M} \end{equation} so we have a 1.75 molar solution.

We also work with units other than litres (L) when dealing with liquids such as millilitres (ml). We have to remember that our formula uses the volume of liquid in litres so if we are told the volume in millilitres and we want to work out the concentration, we first have to convert our volume in millilitres to a volume in litres. For more information on how to do this, see the section on dimensions.

Example 7

Half a mole of a substance is dissolved in 250ml of a liquid to make a solution, what is the concentration of the solution in M (mol/L)?

Solution

Our formula tells us that \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)} \end{equation} and we know that we have 250ml of solution so we first need to work out what this is in litres. There are 1000ml in 1L so to get the volume in litres, we divide 250 by 1000 to get \begin{equation} \frac{250}{1000} = 0.25\text{L}. \end{equation} We can now work out the concentration as before, we have half a mole of substance in 0.25L of liquid so the concentration is \begin{equation} \frac{0.5}{0.25} = 2\text{M}. \end{equation}

If we know the volume of solution and the concentration, we can work out the number of moles of the substance dissolved by rearranging the formula \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)}. \end{equation} to get

Example 8

How many moles of glucose are there in 3L of a 0.5M solution?

Solution

Using our formula, we find that there are \begin{equation} 3 \times 0.5 = 1.5 \text{ moles} \end{equation} of glucose in 3L of a 0.5M solution.

Example 9

How many moles of sodium chloride are there in 50ml of a 5M solution?

Solution

Our formula uses volume in litres so we need to convert 50ml to a volume in litres. There are 1000ml in 1L so 50ml is equal to \begin{equation} \frac{50}{1000} = 0.05\text{L}. \end{equation} Using our formula, we find that the number of moles of sodium chloride in the solution is \begin{equation} 0.05 \times 5 = 0.25 \text{ moles}. \end{equation}

A longer example:

Example 10

Glucose (C₆H₁₂O₆) has a molecular weight of 180.16, what mass of glucose would you need to dissolve in 500ml of water to get a 3M solution?

Solution

Let's break this question up into parts. First we need to know how many moles of glucose we need to get a 3M solution using 500ml of water. Our formula uses volume in litres so we have to convert 500ml to a volume in litres, doing this we find that 500ml equals \begin{equation} \frac{500}{1000} = 0.5\text{L}. \end{equation} To find the number of moles we need to get a 3M solution using 0.5L (500ml) of water, we use the formula \begin{equation} \text{volume of liquid (in litres)} \times \text{concentration (in mol/L)} = \text{number of moles of substance}. \end{equation} Putting in our numbers, we find that we need \begin{equation} 0.5 \times 3 = 1.5 \text{ moles} \end{equation} of glucose. Finally, to work out the mass of glucose we need, we use the formula \begin{equation} \text{molecular weight} \times \text{number of moles} = \text{mass of substance}. \end{equation} We are told in the question that the molecular weight of glucose is 180.16, so putting in our numbers we find that we need \begin{equation} 180.16 \times 1.5 = 270.24\text{g} \end{equation} of glucose. That is, if we dissolve 270.24g of glucose in 500ml (0.5L) of water we will get a 3M solution.

Let's also look at an example that deals with mass concentration.

Example 11

318g of Sodium carbonate is dissolved in 1500ml of water. What is the concentration in g/L?

Solution

We are asked the concentration in g/L and our volume has been given in ml so first we must convert 1500ml to a volume in litres. There are 1000ml in 1L so 1500 ml is equal to \begin{equation} \frac{1500}{1000} = 1.5 \text{ L}. \end{equation} Putting our numbers into the formula \begin{equation} \frac{\text{mass of substance (in grams)}}{\text{volume of liquid (in litres)}} = \text{concentration (in g/L)} \end{equation} we find that the concentration in g/L is \begin{equation} \frac{318}{1.5} = 212 \text{ g/L}. \end{equation}

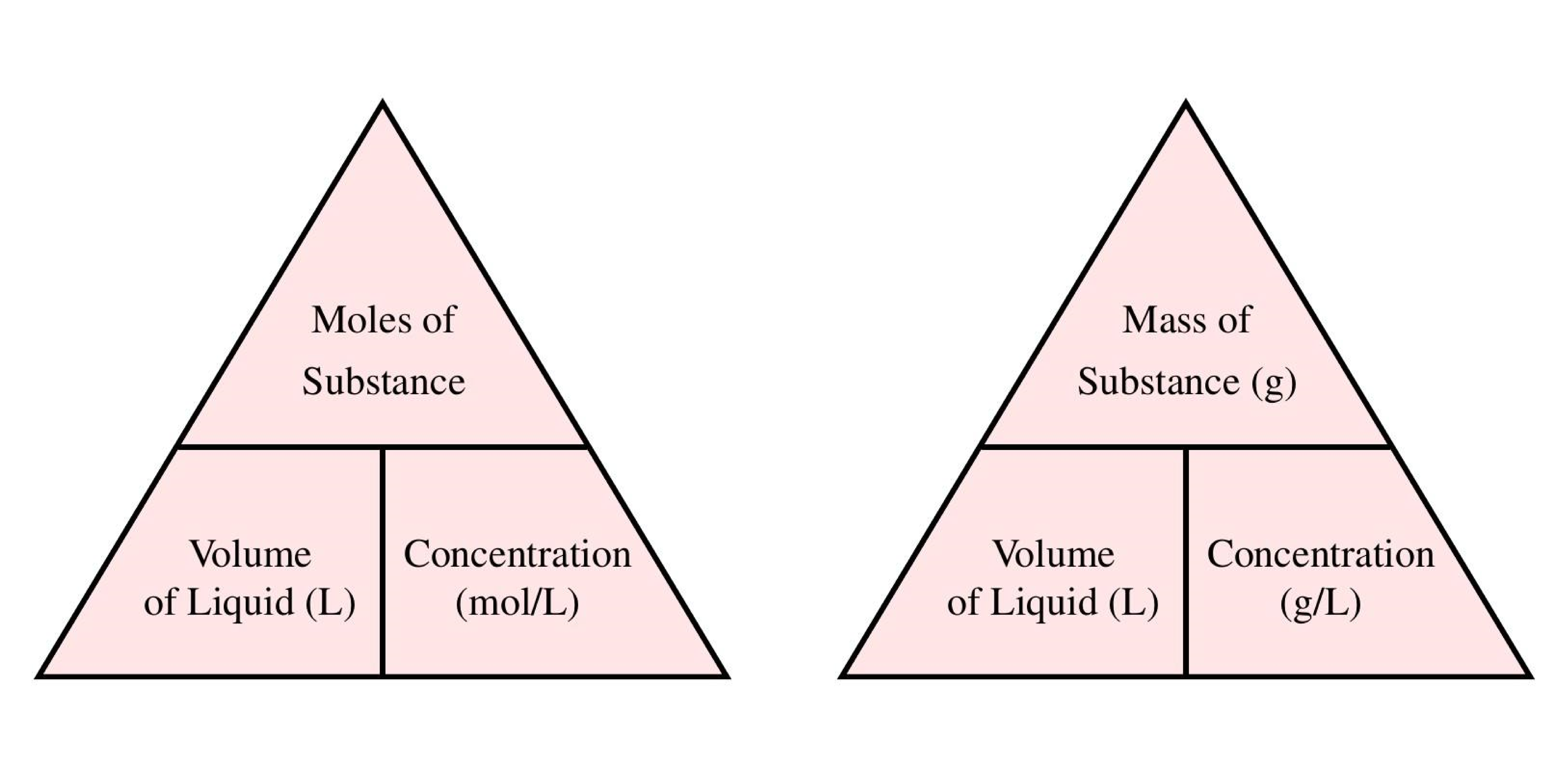
Formula Triangles

To remember the formulas in this section, you can use the formula triangles. To get the formula from the triangle, cover up the value you want to calculate and use the remaining two values. If they are next to each other, multiply them to get the answer, if one is on top of the other, divide the top one by the bottom one to get the answer. Make sure you are using the correct triangle depending on whether you want the concentration to be in mol/L or g/L!

Test yourself

Numbas test on solutions

Diluting Solutions

If we have a solution of a given concentration, we can add more liquid (without adding any more of the substance) to dilute the solution. This lowers the concentration of the solution. For example, if we have 500ml of a 1M solution of glucose in water, we could add another 500ml of water to dilute the solution. We can work out the concentration of the diluted solution in the following way. The formula for the concentration of a solution is \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)}. \end{equation} We started with 500ml of solution and then added another 500ml of water so now the total volume of liquid in the solution is \begin{equation} 500 + 500 = 1000 \text{ ml} \end{equation} which is equal to 1L. We also need to know how many moles of glucose there are in the solution. We started with 500ml of a 1M solution and we have not added any more of the substance (glucose) so we still have the same number of moles that we started with. We can calculate this using the formula \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)}, \end{equation} remembering that the volume is given in litres in this formula, not ml and that 500ml = 0.5L. The number of moles we started with is equal to the number of moles of glucose in 0.5L (500ml) of a 1M solution which is \begin{equation} 1 \times 0.5 = 0.5 \text{ moles}. \end{equation} This means that we started with 0.5 moles of glucose in 0.5L (500ml) of water and then added another 500ml of water to dilute the solution so we now have 0.5 moles of glucose in 1L (1000ml) of water. We now use the formula \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)}. \end{equation} to find the new concentration which is \begin{equation} \frac{0.5}{1} = 0.5 \text{ M}. \end{equation} This is half the concentration we started with. As we might expect, if we start with a solution of a given concentration and then dilute it by doubling the total volume of liquid (we went from 500ml to 1000ml) without adding any more of the substance, the new concentration is half the concentration we started with.

Example 12

20ml of a 0.25M solution is diluted by adding another 480ml of liquid, what is the new concentration in M (mol/L)?

Solution

We started with 20ml of liquid and added another 480ml so the new volume of liquid is \begin{equation} 20 + 480 = 500 \text{ ml}. \end{equation} 20ml is equal to \begin{equation} \frac{20}{1000} = 0.02 \text{ L} \end{equation} so the number of moles we started with is \begin{equation} 0.02 \times 0.25 = 0.005 \text{ moles}. \end{equation} We haven't added any more of the substance so we still have 0.005 moles but this is now dissolved in 500ml of liquid. 500ml is equal to 0.5L so the new concentration is \begin{equation} \frac{0.005}{0.5} = 0.01 \text{ M}. \end{equation}

Note

Another way of asking this question is to say the following:

20ml of a 0.25M solution is diluted to 500ml, what is the new concentration in M (mol/L)?

'Diluted to 500ml' means add enough liquid so that the new volume of liquid is 500ml. We can work out the new concentration in the same way but the first step of working out the new total volume of liquid (500ml) is already done. If we were asked to make this solution up we would need to calculate how much liquid we need to add to make the new total 500ml. In the example above, we started with 20ml of a 0.25M solution so to dilute it to 500ml we would need to add another \begin{equation} 500 - 20 = 480 \text{ ml} \end{equation} of liquid.

Let's look at an example that combines several of the ideas we have learned.

Example 13

A “stock” solution contained 318g of sodium carbonate (Na₂CO₃) in 1L of solution. 50ml of the “stock” solution was diluted to 250ml. What is the concentration of the final solution in g/L and M (mol/L). [The required relative atomic masses (Da) are: Na 22.990; C 12.011; O 15.999].

Solution

We have been asked to do quite a lot of calculations in this example so let's break it up into several smaller parts. To work out the concentrations in g/L and M after dilution, we need to first work out the concentrations in g/L and M of the “stock” solution. Let's start by working out the concentration of the “stock” solution in g/L.

The “stock” solution contains 318g of sodium carbonate dissolved in 1L of liquid. To work out the concentration in g/L we use the formula \begin{equation} \frac{\text{mass of substance (in grams)}}{\text{volume of liquid (in litres)}} = \text{concentration (in g/L)}. \end{equation} Putting in our numbers we find that the concentration of the “stock” solution in g/L is \begin{equation} \frac{318}{1} = 318 \text{ g/L}. \end{equation}

Next, we can work out the concentration of the stock solution in M (mol/L). The formula for this is \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)}. \end{equation}

We can see that we need to work out how many moles of sodium carbonate (Na₂CO₃) there are in 318g. The formula for this is \begin{equation} \frac{\text{mass of substance (in grams)}}{\text{molecular weight}} = \text{number of moles}. \end{equation}

We can see that to do this, we are going to need to work out the molecular weight of sodium carbonate (Na₂CO₃). We have been told the atomic weights of each of the atoms in sodium carbonate (Na₂CO₃) so we can do this by adding together the atomic weights of all the atoms to get the molecular weight which is \begin{equation} 2 \times 22.990 + 1 \times 12.011 + 3 \times 15.999 = 82.998 \text{ Da}. \end{equation}

We can now use this to work out how many moles of sodium carbonate there are in 318g using the formula above. Putting in the numbers we find that there are \begin{equation} \frac{318}{82.998} = 3.831 \text{ moles to 3 d.p. (decimal places)} \end{equation} of sodium carbonate in 318g. We can now work out the concentration of the “stock” solution in M (mol/L). The formula is \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)}. \end{equation} We have 318g of sodium carbonate dissolved in 1L of liquid and we have calculated that there are 3.831 moles of sodium carbonate in 318g. Putting these numbers into the formula we find that the concentration of the “stock” solution in M is \begin{equation} \frac{3.831}{1} = 3.831 \text{ M}. \end{equation}

Let's recap what we have calculated so far. We have worked out that the concentration of the “stock” solution in g/L is \begin{equation} 318 \text{ g/L} \end{equation} and in M is \begin{equation} 3.831 \text{ M}. \end{equation}

Since we are diluting 50ml of the “stock” solution, we need to work out how much sodium carbonate there is in 50ml of the solution using the concentrations we have calculated. We need to work this amount out in both grams and moles, let's start with grams. If we rearrange the formula \begin{equation} \frac{\text{mass of substance (in grams)}}{\text{volume of liquid (in litres)}} = \text{concentration (in g/L)}. \end{equation} we find that

Now, 50ml is equal to \begin{equation} \frac{50}{1000} = 0.05 \text{ L}, \end{equation} so in 50ml of “stock” solution, there are \begin{equation} 0.05 \times 318 = 15.9 \text{ g} \end{equation} of sodium carbonate. Similarly, we can work out the number of moles of sodium carbonate using the formula \begin{equation} {\text{volume of liquid (in litres)}} \times \text{concentration (in mol/L)} = \text{number of moles of substance}. \end{equation}. Putting in our numbers, we find that in 50ml of “stock” solution, there are \begin{equation} 0.05 \times 3.831 = 0.192 \text{ moles to 3 d.p.} \end{equation} of sodium carbonate.

Finally, we can work out the concentration of the diluted solution. We know that 50ml of “stock” solution is diluted to 250ml so the final volume of liquid is 250ml. We have worked out that in 50ml of stock solution there are 15.9g (0.192 moles) of sodium carbonate and we have not added any more sodium carbonate so in our diluted solution we have 15.9g (0.192 moles) of sodium carbonate in 250ml of liquid. The formula for the concentration in g/L is \begin{equation} \frac{\text{mass of substance (in grams)}}{\text{volume of liquid (in litres)}} = \text{concentration (in g/L)}. \end{equation} 250ml is equal to 0.25L and so the concentration of the diluted solution in g/L is \begin{equation} \frac{15.9}{0.25} = 63.6 \text{ g/L}. \end{equation} The formula for concentration in M (mol/L) is \begin{equation} \frac{\text{number of moles of substance}}{\text{volume of liquid (in litres)}} = \text{concentration (in mol/L)} \end{equation} so the concentration of the diluted solution in M is \begin{equation} \frac{0.192}{0.25} = 0.766 \text{ M to 3 d.p.} \end{equation}

Test yourself

Numbas test on diluting solutions

Test yourself

If you would like to test yourself on all the topics in this article, the following link contains all of the numbas questions that accompany this article.

Numbas test on molar calculations