Equation of a Straight Line
Definition
The equation of a straight line is \[y = mx + c\] $m$ is the gradient and $c$ is the height at which the line crosses the $y$-axis, also known as the $y$-intercept.
The gradient $m$ is the slope of the line - the amount by which the $y$-coordinate increases in proportion to the $x$-coordinate. If you have two points $(x_1,y_1)$ and $(x_2,y_2)$ on the line, the gradient is \[m = \dfrac{y_2 - y_1}{x_2 - x_1}\]
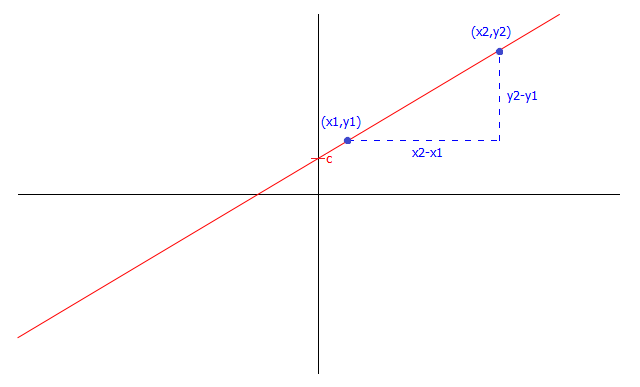
|center
If you know one point $(x_1,y_1)$ on the line as well as its gradient $m$, the equation of the line is \[(y - y_1) = m(x - x_1)\]
If we are just given two points $(x_1, y_1)$ and $(x_2, y_2)$, we must first work out the gradient using the gradient formula above, and then choose either point to substitute into the straight line equation with this gradient.
Worked Examples
Example 1
Find the equation of the line with gradient $-2$ that passes through the point $(3,-4)$.
Solution
Put $m=-2$, $x_1=3$ and $y_1=-4$ straight into the formula $y-y_1=m(x-x_1)$.
\[y-y_1=m(x-x_1)\] \[y+4=-2(x-3)\]
Expand the brackets and simplify.
\[y+4=-2x+6\] \[y=-2x+2\]
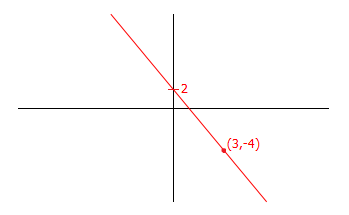
|center
Example 2
Find the equation of the straight line through the points $(-5,7)$ and $(1,3)$.
Solution
First, find the gradient by substituting the coordinates $x_1 = -5$, $y_1 = 7$, $x_2=1$ and $y_2=3$ into the formula for the gradient:
\begin{align} m &= \frac{y_2-y_1}{x_2-x_1}\\\\ &= \frac{3-7}{1-(-5)}\\\\ &= \frac{-4}{6}\\\\ &= -\frac{2}{3} \end{align}
Choose either point and put into the formula $y-y_1=m(x-x_1)$:
\begin{align} y-y_1 &= m(x-x_1) \\ y-7 &= - \frac{2}{3}(x-(-5)) \end{align}
Expand the brackets and simplify.
\begin{align} y - 7 &= -\frac{2}{3}x - \frac{10}{3} \\ y &= -\frac{2}{3}x +\frac{11}{3} \end{align}
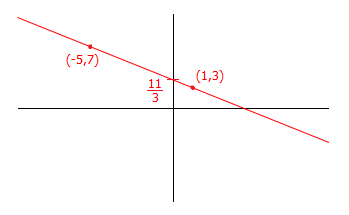
|center
Video Examples
Example 1
Prof. Robin Johnson finds the equation of the straight line through the points $(1,2)$ and $(-3,4)$.
Example 2
Prof. Robin Johnson finds the equation of the straight line with gradient $m=-3$ that passes through the point $(-1,2)$.
Example 3
Hayley Bishop finds the equation of the straight line through the points $(0,2)$ and $(-1,4)$.
Workbook
This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.
Test Yourself
Test yourself: Find the equation of a line through two points
External Resources
- The gradient of a straight line segment workbook at mathcentre.
- Equations of straight lines workbook at mathcentre.