Sine, Cosine and Tangent
Sine
Definition
Sine is an odd function and is periodic with period $2\pi$. The sine function has a domain of all real numbers, and its range is $-1\leq \sin x \leq 1$.
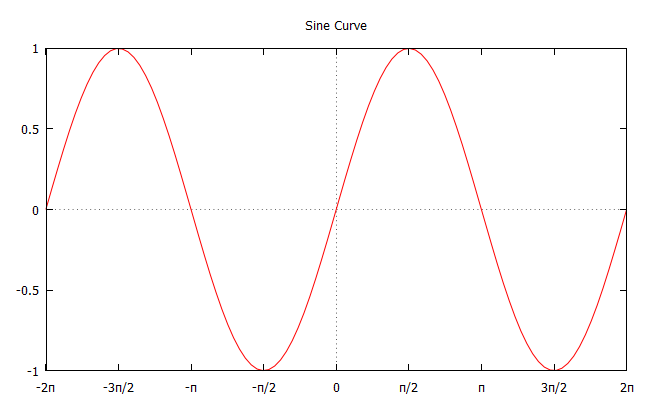
|center
Cosine
Definition
Cosine is an even function function and is periodic with period $2\pi$. The cosine function has a domain of all real numbers, and its range is $-1\leq \cos x \leq 1$.
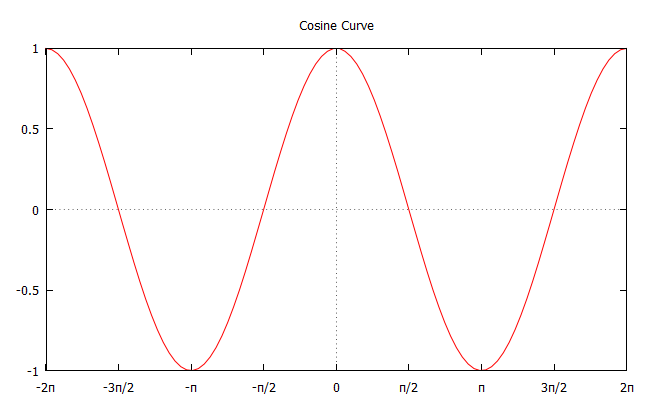
|center
Tangent
Definition
The tangent function repeats in intervals of $\pi$ and has asymptotes every multiple of $\dfrac{n\pi}{2}$ for odd $n$. The tangent function has all real numbers except odd multiples of $90^{\circ}$ or $\pi/2$ in its domain, and its range contains all real numbers.
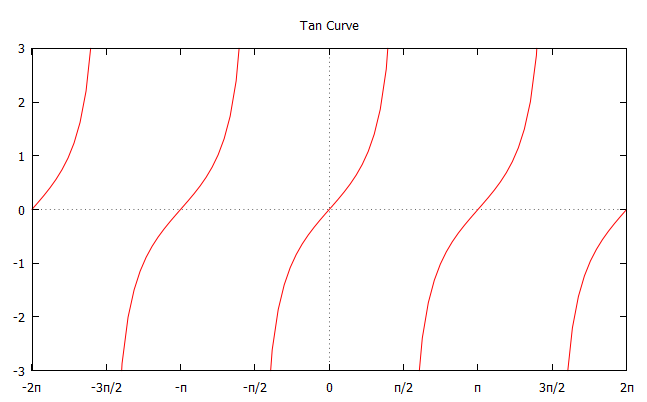
|center
Tangent is defined to be \[\tan x = \dfrac{\sin x}{\cos x}.\]
Common Trig Ratios
Here is a table of common angles and the values of their corresponding trigonometric ratios.
$x$ |
$0$ |
$\dfrac{\pi}{6}$ |
$\dfrac{\pi}{4}$ |
$\dfrac{\pi}{3}$ |
$\dfrac{\pi}{2}$ |
|---|---|---|---|---|---|
$\sin x$ |
$\;\;0\;\;$ |
$\;\,\dfrac{1}{2}$ |
$\dfrac{1}{\sqrt{2}}$ |
$\dfrac{\sqrt{3}}{2}$ |
$\;\;1\;\;$ |
$\cos x$ |
$\;\;1\;\;$ |
$\dfrac{\sqrt{3}}{2}$ |
$\dfrac{1}{\sqrt{2}}$ |
$\;\,\dfrac{1}{2}$ |
$\;\;0\;\;$ |
$\tan x$ |
$\;\;0\;\;$ |
$\dfrac{1}{\sqrt{3}}$ |
$\;\;1\;\;$ |
$\sqrt{3}$ |
$\;\infty\;$ |
Derivatives
Trig functions can be differentiated and integrated.
$f(x)$ |
$f'(x)$ |
|---|---|
$\sin x$ |
$\cos x$ |
$\cos x$ |
$-\sin x$ |
$\tan x$ |
$\sec^2 x$ |
Inverses
The inverses of these trigonometric functions are $\arcsin, \; \arccos, \; \arctan$, although they are also sometimes written as $\sin^{-1}, \; \cos^{-1}, \; \tan^{-1}$.
Video Examples
Example 1 - Sine
Prof. Robin Johnson sketches the graph of $\sin x$.
Example 2 - Tangent
Prof. Robin Johnson sketches the graph of $\tan x$.
Workbook
This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.
See Also
External Resources
- Graphs of the trig functions workbook at mathcentre.