Box and Whisker Plots

Definition

A box and whisker plot or diagram (otherwise known as a boxplot), is a graph summarising a set of data. The shape of the boxplot shows how the data is distributed and it also shows any outliers. It is a useful way to compare different sets of data as you can draw more than one boxplot per graph. These can be displayed alongside a number line, horizontally or vertically.

Reading a Box and Whisker Plot

Interpreting a boxplot can be done once you understand what the different lines mean on a box and whisker diagram. The line splitting the box in two represents the median value. This shows that $50$% of the data lies on the left hand side of the median value and $50$% lies on the right hand side. The left edge of the box represents the lower quartile; it shows the value at which the first $25$% of the data falls up to. The right edge of the box shows the upper quartile; it shows that $25$% of the data lies to the right of the upper quartile value. The values at which the horizontal lines stop at are the values of the upper and lower values of the data. The single points on the diagram show the outliers.

Video Examples
Example 1

This is a video on how to interpret a boxplot produced by Alissa Grant-Walker.

Example 2

This is a video by Khan Academy on reading box and whisker diagrams.

Constructing a Box and Whisker Diagram

First of all outliers are plotted against the number line. The main body of the box is made up of three lines: the first indicating the lower interquartile value, and the middle indicating the median and the third showing the upper interquartile value. The 'whiskers' are created by are straight lines extending from the ends of the box to the maximum and minimum values (excluding the outliers.)

Worked Example

Worked Example

Draw a Box and Whisker diagram for the number of books taken out of the library per month by first year students and compare this with the box and whisker diagram for the number of books taken out of the library per month by third year students.

The number of books taken out of the library per month by first year students from a sample of $15$ is as follows:

\[3,\ 0,\ 12,\ 0,\ 2,\ 0,\ 26,\ 0,\ 7,\ 5,\ 5,\ 2,\ 1,\ 1,\ 2.\]

The number of books taken out of the library per month by third year students from a sample of $15$ is as follows: \[12,\ 0,\ 9,\ 4,\ 15,\ 2,\ 6,\ 10,\ 27,\ 15,\ 5,\ 9,\ 1,\ 14,\ 2.\]

Solution

First of all start by ordering the data.
The number of books taken out of the library per month by first year students from a sample of $15$ is as follows: \[0,\ 0,\ 0,\ 0,\ 1,\ 1,\ 2,\ 2,\ 2,\ 3,\ 5,\ 5,\ 7,\ 12,\ 26.\]

The number of books taken out of the library per month by third year students from a sample of $15$ is as follows: \[0,\ 1,\ 2,\ 2,\ 4,\ 5,\ 6,\ 9,\ 9,\ 10,\ 12,\ 14,\ 15,\ 15,\ 27.\]

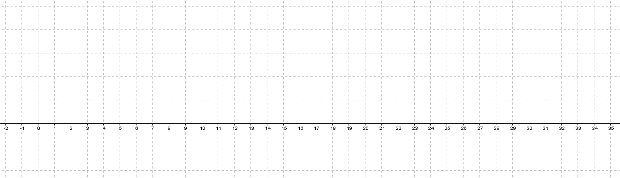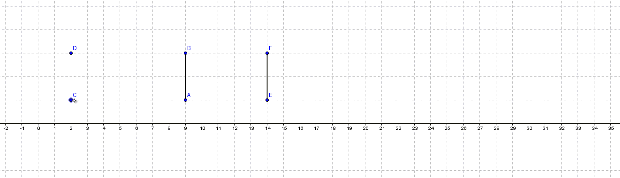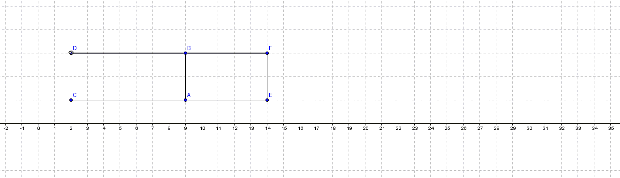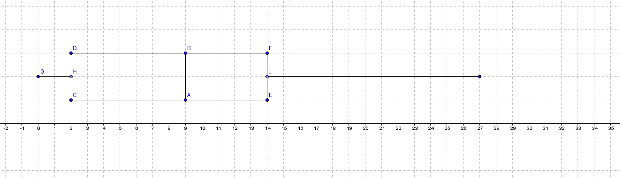
Next, work out the median and interquartile values and use these to find any outliers. Plot these against a number line as a line and connect the median and quartiles together to make a box shape. Draw a point to represent the upper and lower values, with a straight line join these up to the edges of the box. Plot the outliers as a point on the diagram.

|250px

|250px

For first year students the data is as follows:
Sample size: $15$,
Median: $2$,
Minimum value: $0$,
Maximum value: $26$,
First quartile: $0$,
Third quartile: $5$,
Interquartile Range: $5$,
Outliers: $26$.
For third year students the data is as follows:
Sample size: $15$,
Median: $9$,
Minimum value: $0$,
Maximum value: $27$,
First quartile: $2$,
Third quartile: $14$,
Interquartile Range: $12$,
Outliers: none.

For help on working these out see Other Measures of Dispersion and Mean, Median and Mode.
You can plot the two boxplots on the same diagram to compare them easier.

Video Example
Example 1

This is a video on how to construct boxplots produced by Alissa Grant-Walker.

Example 2

This is Khan Academy's video on box and whisker plots.

Common Mistakes

Common mistake include missing data when performing the process of ordering data and using the mean instead of the median to represent the middle value. To avoid these mistakes, count the number of pieces of data you have and ensure you have the same amount after you have rearranged them.

Workbook

This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.

Test Yourself

External Resources