Types of Correlation
Definition
Correlation describes the relationship between variables. It can be described as either strong or weak, and as either positive or negative.
Note: 1= Correlation does not imply causation.
Positive Linear Correlation
There is a positive linear correlation when the variable on the $x$-axis increases as the variable on the $y$-axis increases. This is shown by an upwards sloping straight regression line.
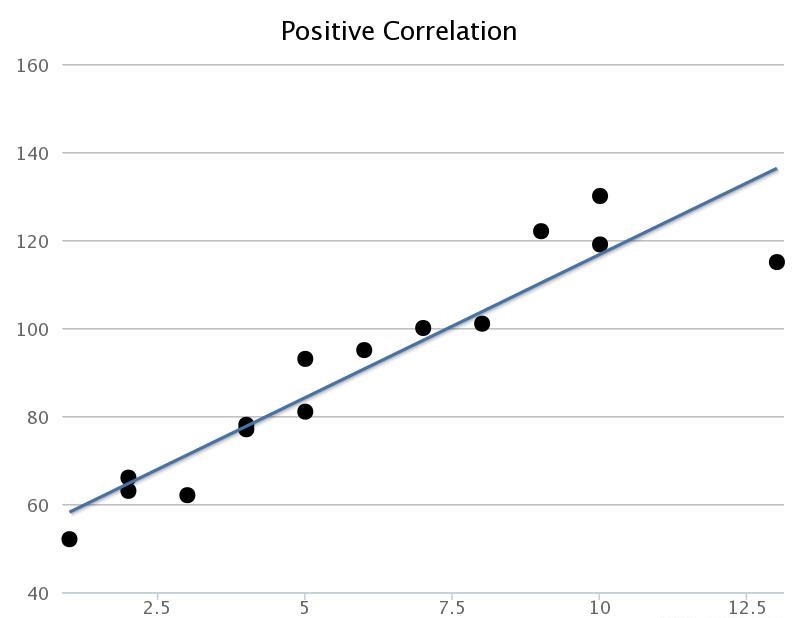
|225px|text-top|Positive Correlation
Negative Linear Correlation
There is a negative linear correlation when one variable increases as the other variable decreases. This is shown by a downwards sloping straight regression line.
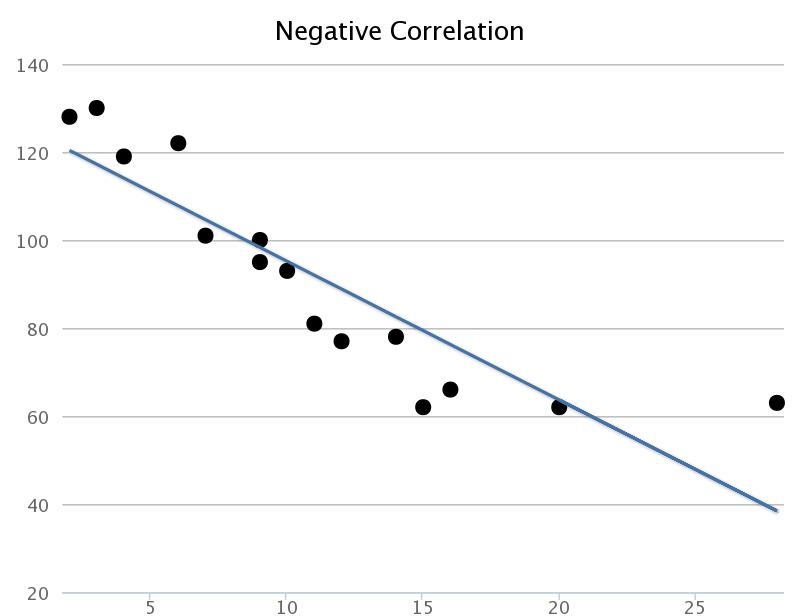
|225px|text-top|Negative Correlation
Non-linear Correlation (known as curvilinear correlation)
There is a non-linear correlation when there is a relationship between variables but the relationship is not linear (straight).
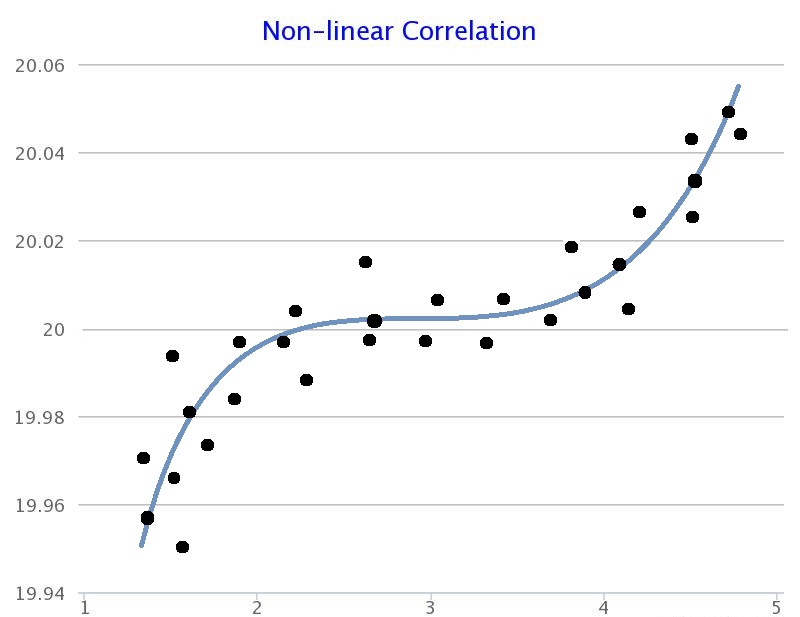
|225px|text-top|Non-linear Correlation
No Correlation
There is no correlation when there is no pattern that can be detected between the variables.
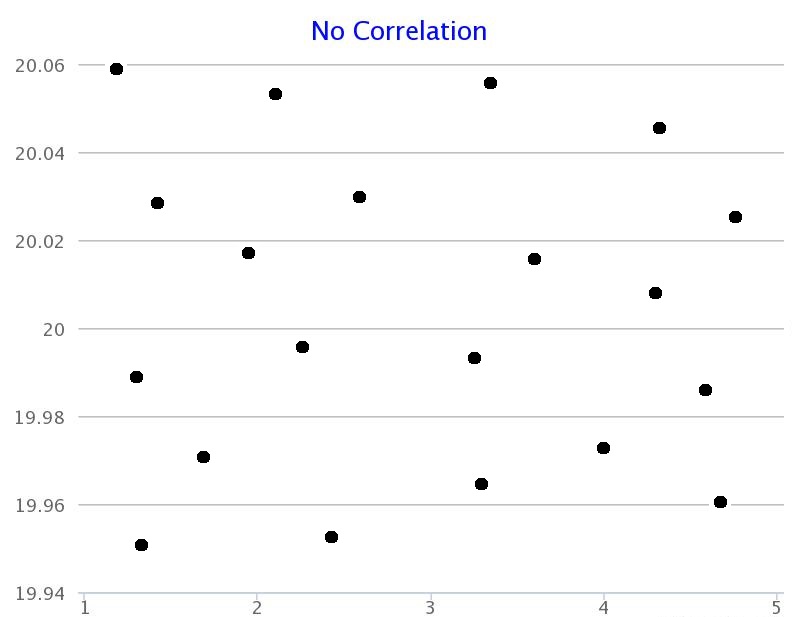
|225px|text-top|No Correlation
Worked Example
Worked Example
The local ice-cream shop have kept track of how much ice-cream they sell and the maximum temperature on that day. The data that they obtained during the last 15 days is as follows:
|
Temperature (°c) |
Ice-cream Sales (£) |
|---|---|
|
$12.5$ |
$211$ |
|
$15.8$ |
$230$ |
|
$22.1$ |
$359$ |
|
$18.9$ |
$284$ |
|
$17.7$ |
$254$ |
|
$19.3$ |
$287$ |
|
$15.3$ |
$248$ |
|
$19.2$ |
$303$ |
|
$13.4$ |
$235$ |
|
$14.1$ |
$209$ |
|
$16.7$ |
$267$ |
|
$18.6$ |
$295$ |
|
$11.9$ |
$199$ |
|
$18.4$ |
$274$ |
|
$18.9$ |
$279$ |
Determine the type of correlation between the number of ice-cream sales and the maximum temperature of the day.
Solution
Firstly draw a scatter diagram with the given data.
.png)
|300x350px|texttop|Ice-cream Sales vs Maximum Temperature.
This shows that there is strong positive linear correlation between ice-cream sales and maximum temperature. However, it is not always as easy to tell just by looking at the scatter graph, instead we quantify it using a numeric value known as the correlation coefficient.
Test Yourself
External Resources
- Types of Correlation at BBC Bitesize
- Correlation at