Quadratic Equations and Functions (Economics)

Quadratic Equations

A quadratic equation is an equation of the general form \[ax^2+bx+c=0\] where $a\neq 0$ where $x$ is a variable and $a,b$ and $c$ are constants.

In other words, it is an equation where the highest power of the variable (usually $x$) is $2$.

Solving a quadratic equation means finding values of $x$ which satisfy the equation (make the expression on the left-hand side of the $=$ sign equal to zero). These values of $x$ are called the solutions to the quadratic equation. Quadratic equations can have two, one or no real solutions. The solutions of a quadratic equation correspond to the roots of a quadratic function.

There are two commonly-used methods of solving quadratic equations: factorisation and the quadratic formula.

Factorisation

In some cases it is possible to write the quadratic expression on the left-hand side of a quadratic equation as a product of two linear expressions each enclosed in a pair of brackets. Writing the quadratic in this way is known as factorising the quadratic or simply factorisation because it involves finding the factors of the quadratic expression.

For example, factorising the left hand side of the quadratic equation $x^2+(r+s)x+rs=0$ gives $(x+r)(x+s)$. The roots of this equation are therefore $(-r)$ and $(-s)$ since we can see that when we substitute either of these values for $x$ the expression in one of the pairs of brackets becomes equal to zero (check!), so the equation is satisfied.

We know that factorisation is the reverse of expanding brackets. Expanding the brackets is therefore a useful way to check whether you have factorised a quadratic expression correctly. Check for yourself that the above factorisation is correct by expanding the brackets.

Note: It is not always possible to factorise a quadratic expression. However when it is possible, the factorisation method is typically preferred to using the quadratic formula because it is faster.

===Method: when $a=1$===

Suppose we are asked to solve a quadratic of the form $x^2+bx+c=0$ by factorisation. For example, $x^2+5x+6=0$. To do this, we must find $2$ numbers, call them $A$ and $B$, which multiply together to give $6$ and sum to give $5$.

The factorisation of $x^2+5x+6$ is then $(x+A)(x+B)$ and the roots of the equation are $(-A)$ and $(-B)$. A good way to keep track of the possibilities for $A$ and $B$ is to make a table which lists all of the values for $A$ and $B$ whose product is $6$:

$A$

$B$

$AB$

$A+B$

1

6

6

7

(-1)

(-6)

6

(-7)

2

3

6

5

(-2)

(-3)

6

(-5)

Note: For each pair of numbers, it doesn’t matter which we put in the “A column” and which we put in the “B column”.

We can see from the table above that the only pair of values whose product is $6$ and which sum to $5$ are $2$ and $3$. The factorisation of $x^2+5x+6$ is thus \[(x+2)(x+3)=0\] and the roots of the equation are $(-2)$ and $(-3)$.

Note: We can check that these are indeed the roots of $x^2+5x+6=0$ by substituting them into the equation: \[(-2)^2+5\times(-2)+6=4-10+6=0\] \[(-3)^2+5\times(-3)+6=9-15+6=0\] Both $(-2)$ and $(-3)$ satisfy the equation so these are the roots of the equation.

Method: when $a\neq1$

Suppose we are asked to factorise and solve a quadratic of the form $ax^2+bx+c=0$ where $a\neq1$ and $a\neq0$.

To solve any equation of this form, we take the $a$ outside brackets to give: \[a\left(x^2+\frac{b}{a}x+\frac{c}{a}\right)=0\] If the expression in the brackets contains only integer coefficients, we can then use the method above to factorise the expression inside the brackets and so solve the equation.

Example 1

Suppose we are asked to solve the equation $5x^2-25x+30=0$. Rewriting this equation with $a=5$ outside brackets gives: \[5(x^2-5x+6)=0\] We can then factorise the expression inside the brackets as follows (see the example above for how to do this): \[x^2-5x+6=(x-3)(x-2)=0\] So the factors are $(x-2)$ and $(x-3)$. However, recall that the original equation was \[5(x^2-5x+6)=0\] which can now be written as \[5(x-3)(x-2)=0\] so we can see that $5$ is another factor. The solutions to the equation are $x=2$ and $x=3$.

Video Example

Prof. Robin Johnson factorises the expression $x^2+x-6$.

The Quadratic Formula

The quadratic formula can be used to solve any quadratic expression of the form $ax^2+bx+c=0$ (where $a\neq0$). The formula is: \[x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\]

Not only can we use this formula directly to determine the solutions (or roots) of a quadratic, but the expression inside the square root (called the discriminant) tells us how many solutions we can expect to find and whether or not it is possible to factorise the quadratic:

  • If $b^2-4ac\gt0$ there are two distinct real roots and it is possible to factorise the quadratic.
  • If $b^2-4ac=0$ then there is only one root (called a repeated real root) and we cannot factorise the quadratic.
  • $b^2-4ac\lt0$ there are no real roots (each root will contain an imaginary number).

See The Quadratic Formula for more information and examples of using the quadratic formula to solve quadratic equations.

Simultaneous Quadratic Equations

We can solve pairs of simultaneous quadratic equations. See Solving Simultaneous Linear Equations (Economics) for a reminder on how to solve simultaneous equations. Simultaneous quadratic equations can have up to $2$ pairs of solutions.

Worked Example

Solve the following pair of simultaneous equations: \[x^2+y^2=29\] \[y-x=3\]

Solution

Here we will use the substitution method. Let's first label the equations: \[x^2+y^2=29\;\;\;\textbf{(1)}\] \[y-x=3\;\;\;\textbf{(2)}\] Since equation $\textbf{(1)}$ contains $x^2$ and $y^2$ as variables, it is easier to rearrange equation $\textbf{(2)}$ to make either $x$ or $y$ the subject and then substitute this into equation $\textbf{(1)}$. Rearranging equation $\textbf{(2)}$ to make $y$ the subject gives: \[y=3+x\;\;\;\textbf{(2)}\] We can now substitute this directly into equation $\textbf{(1)}$: \begin{align} &x^2+(3+x)^2=29\\ \Rightarrow &2x^2+6x+9=29\\ \Rightarrow &2x^2+6x-20=0 \end{align} We now have a single quadratic equation which we can solve using the methods discussed above. Since this equation is difficult to factorise, we will use the quadratic formula. This gives $x=-5$ or $x=2$ (check for yourself). Substituting $x=-5$ into equation $\textbf{(2)}$ gives: \begin{align} y&-(-5)=3\\ \Rightarrow &y=-2 \end{align} So $x=-5$ and $y=-2$ is one solution. We will now find the other solution. Substituting $x=2$ into equation $\textbf{(2)}$ gives: \begin{align} y&-2=3\\ \Rightarrow &y=5 \end{align} So the other solution is $x=2$ and $y=5$.

Quadratic Functions

A quadratic function is a function of the general form \[y = ax^2+bx+c\] where $a$, $b$ and $c$ are real numbers and $a\neq0$. These functions are called quadratic as $x$ is raised to the power of $2$.

The roots of a linear function are the values of $x$ which make the right-hand side of the function equal to zero. That is, the value of $x$ which satisfy: \[ax^2+bx+c=0\] The roots of a quadratic function correspond to the solutions of a quadratic equation. Quadratic functions can have two, one or no real roots. We can find the roots of a quadratic function by solving the equation $ax^2+bx+c=0$ using either factorisation or the quadratic formula.

The graph of a quadratic function is “U-shaped” and is called a parabola. The point where the parabola changes direction is called the turning point of the function.

If $a\gt0$, then we have an upwards-opening parabola which looks like this $\cup$ and the turning point is called a global minimum because it is the point where the graph of the function is at its lowest.

If $a\lt0$, then we have an downwards-opening parabola which looks like this $\cap$ and the turning point is called a global maximum because it is the point where the graph of the function is at its highest.

The absolute value of $a$ determines how steeply the parabola curves. The greater the absolute value of $a$, the steeper the curve is.

If $b=0$, the parabola goes through the origin (where $x$ and $y$ are both equal to zero).

The value of $c$ is the $y$-axis intercept. The $x$-axis intercept(s) correspond to the roots of the function (see above).

The best way to plot the graph of a quadratic function is to first make a table with a few $x$ values and the corresponding $y$ values and then plot each of these points.

Cubic Functions

A cubic function is a function of the general form \[y = ax^3+bx^2+cx+d\] where $a$, $b$, $c$ and $d$ are real numbers and $a\neq0$. These functions are called cubic as $x$ is raised to the power of $3$. A cubic function can have up to $3$ roots. The graph of a cubic function is an “S” shape.

If $a\gt 0$, the graph will look like this:

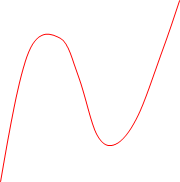
If $a\lt 0$, the graph will look like this:

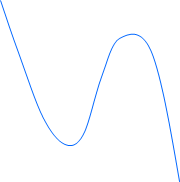
Cubic functions can have up to three real roots. We can find the roots of a cubic function by solving the equation $ax^3+bx^2+cx+d=0$.

Workbook

This workbook produced by HELM is a good revision aid, containing key points for revision and many worked examples.

Test Yourself

Test yourself: Quadratic expressions and equations

External Resources