Z-Test
This is a subject-specific page for Psychology students.
z-tests - Population variance known
$z$-tests are a statistical way of testing a hypothesis, when we know the population variance $\sigma^2$. We use them when we wish to compare the sample mean $\mu$ to the population mean $\mu_0$. However, if your sample size is large, $n \geq 30$, then you can still use $z$-tests without knowing the population variance. Instead, you may use the sample variance as an estimate of the population variance.
These are some conditions for using this type of test:
- The data must be normally distributed.
- All data points must be independent.
- For each sample the variances must be equal.
An example: You want to test the results of a group of $20$ children's average IQ scores against some national data to see if there is a difference. The national data is normally distributed with known variance. A large number of pupils in a school have taken the test and in order to save time she decides to take a random sample of her pupils' results. She calculates the sample mean and then uses a $z$-test to see if there is any significant difference between the sample mean and the national mean. In this case, the null hypothesis would be that there is no significant difference, and the $z$-test is used to see if this is the case or if could it be rejected i.e. there is strong evidence that the means differ.
The $z$-test statistic is calculated using the following formula:
\begin{equation} z = \dfrac{\bar{x} - \mu_0}{\sqrt{\dfrac{\sigma^2}{n}}} \end{equation}
The Method:
- Firstly, identify the null hypothesis $H_0: \mu = \mu_0$ for example, the average IQ of a group of schoolchildren is the same as the national average.
- Then identify the alternative hypothesis $H_1$ and decide if it is of the form $H_1: \mu \neq \mu_0$ (atwo tailed test) or if there is a specific direction for how the mean changes $H_1: \mu > \mu_0$ or $H_1: \mu < \mu_0$, (aone tailed test). For example, the average IQ of the schoolchildren is higher than the national average. (a one-tailed hypothesis). Or, the average IQ of the schoolchildren is different from the national average ( a two-tailed hypothesis).
- Next, calculate the test statistic, using the formula above in the red box.
- Compare the test statistic to the critical values and obtain a range for the $p$ value.
- Form conclusions. If your $z$-statistic is greater than the critical values in the table, it is significant. You can reject the null hypothesis at that level, otherwise you accept it.
For an example of a one-sample $z$-test, see below.
Two sample z-tests
Often, we need to compare the means from two samples and we use the $z$-statistic for when we know the population variances ($\sigma^2$) (see two sample t-tests for unknown variances). There are two types of two sample $z$-test:
- Paired $z$-test/related $z$-test - comparing two equally sized sets of results where they are linked (where you test the same group of participants twice or your two groups are similar) .
- Independent/unrelated $z$-test - where there is no link between the groups (different independent groups).
The main difference between these two tests is that the $z$-statistic is calculated differently.
For the independent/unrelated $z$-test, the test statistic is:
\begin{equation} z = \dfrac{\bar{x_1} - \bar{x_2}}{\sqrt{\dfrac{\sigma_1^2}{n_1} +\dfrac{\sigma_2^2}{n_2}}} \end{equation}
where $\bar{x_1} \text{and } \bar{x_2}$ are the sample means, $n_1 \text{and } n_2$ are the samples sizes and $\sigma_1^2 \text{and } \sigma_2^2$ are the population variances.
For paired/related $z$-tests the $z$-statistic is:
\begin{equation} z= \dfrac{\bar{d}- D}{\sqrt{\dfrac{\sigma_d^2}{n}}} \end{equation}
where $\bar{d} $is the mean of the differences between the samples, $D$ is the hypothesised mean of the differences (usually this is zero), $n$ is the sample size and $\sigma_d^2$ is the population variance of the differences.
- Once you have calculated the test statistic you use the standard normal tables to obtain the critical values, obtain a range for the $p$-value and compare your $z$-statistic. Then form your conclusions. If the $z$-statistic calculated is significant then you can reject the null hypothesis, otherwise you accept it.
The z-Table
This is a $z$-table with an explanation of each section of the table and a guide for using it:
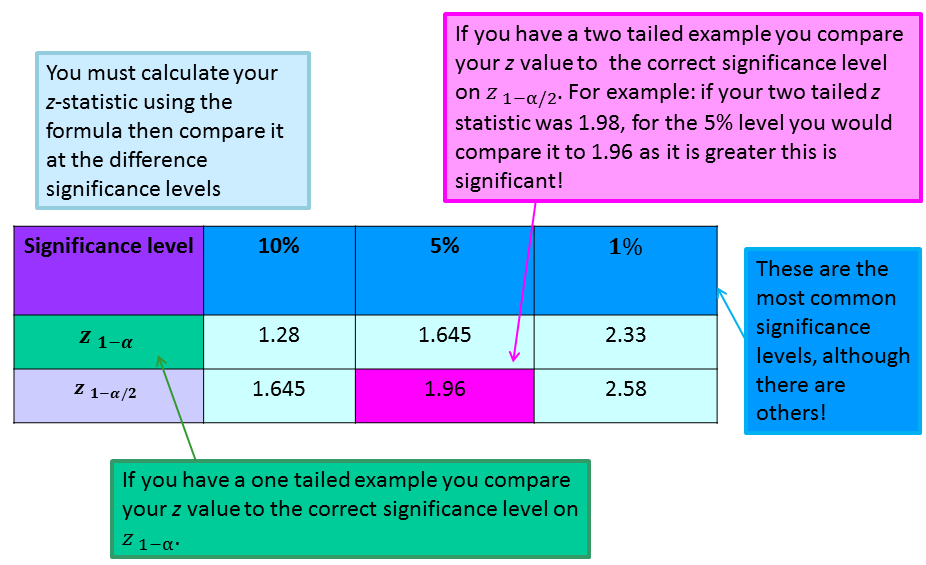
|centre
Worked Example
Worked Example - One Sample z-test
Research for a campaign to increase mental health awareness is being carried out. Using data from all GP practices across the U.K., the number of patients suffering from depression as a percentage of all patients over the past $15$ years was recorded. The mean was found to be $21.9\%$ and the standard deviation was found to be $7.5\%$. In the Liverpool area, data from $35$ GP practices was collected, and the proportion of patients diagnosed with depression was recorded for the past fifteen years. The mean was found to be $26.2\%$.
How would we decide if the proportion of people suffering from depression is different in the Liverpool area than the national average?
Solution
This is an example of a one sample $z$-test, since we know the population mean, $\mu = 21.9$, and the population standard deviation, $\sigma = 7.5$. We also have a sample size of $35$ > $30$, so we could use the sample standard deviation in our calculations. However, we know the population standard deviation, so we shall use it in our calculations.
Our hypotheses are: \begin{align} H_0&: \mu = 21.9\\ H_1&: \mu \neq 21.9\\ \end{align}
So the null hypothesis is that the proportion of people suffering from depression in the Liverpool area is no different from the proportion in the U.K. Whereas the alternative hypothesis is that the proportion of people suffering from depression in the Liverpool area differs from the U.K. average. We have a two tailed test here.
Now we need to calculate our test statistic.
\begin{align} z &= \dfrac{~26.2 - 21.9~}{~\sqrt{\dfrac{7.5^2}{35}~}~}\\ &= \dfrac{4.3}{~\sqrt{1.6071}~}\\ &= 3.39\text{ (2 d.p.).}\\ \end{align}
We compare this to our critical values at the $\alpha$ significance level (we use $z_{1-\alpha/2}$ values, since it is a two-tailed test).
|
Significance Level |
Critical Value |
|---|---|
|
$90\%~(0.1)$ |
1.65 |
|
$95\%~(0.05)$ |
1.96 |
|
$99\%~(0.01)$ |
2.58 |
Since our $z$-value of $3.39$ is greater than $2.58$, we have a significant result at the $1$% level (the $p$ value for $3.39$ is a lot less than $0.01$). Therefore, we have very strong evidence against the null hypothesis. We can conclude that the proportion of people in the Liverpool area suffering from depression is different from the proportion in the U.K.
Alternatively, a more concise way of reporting our findings is as follows.
'It has been found that the proportion of people suffering from depression in Liverpool $(\bar{X} = 26.2\%)$ is different to the national average $(\bar{X} = 21.9\%)$. $(z = 3.39, p < 0.01).$'
Test Yourself
Try our Numbas tests on parametric hypothesis tests and two-sample tests.
See Also
- When variance is unknown use a “t”-test
- Click here for some more worked examples (from the Business page).
- See also non-parametric hypothesis testing and tests on frequencies for information on other types of hypothesis testing.