Parametric Hypothesis Tests (Psychology)
What is a Parametric test?
A parametric test relies upon the assumption that the data you want to test is (or approximately is) normally distributed. Your data needs to be symmetrical, since normally distributed data is symmetrical. If your data does not have the appropriate properties then you use a non-parametric test.
Important Note
The worked examples in this section do not necessarily have the best experimental designs. They are also purely hypothetical and any results or data are not from any real studies, cases nor experiments. The purpose of them is to demonstrate how to use the various hypothesis tests covered in this section.
Different Parametric Tests
There are three main parametric tests
Which Test?
Often it can be difficult to decide whether to use a $z$-test or a t-test as they are both very similar. Here are some tips to help you decide:
- If you have a sample which is very large, (a good guide is $n \geq 30$) then you can use a $z$-test.
- If the population variance $(\sigma^2)$ is known, then we use a $z$ test.
- If the population variance ($\sigma^2$) is unknown and the sample is large then we use a $z$-test. In the test statistic, we replace the population variance $\sigma^2$ with $s^2$.
- If the population variance ($\sigma^2$) is unknown and we have a small sample then we use a t-test.
- If your data is not independent (for instance re-testing the same group) then you use a paired test.
The following diagram can be used to help you decide which test is appropriate too.
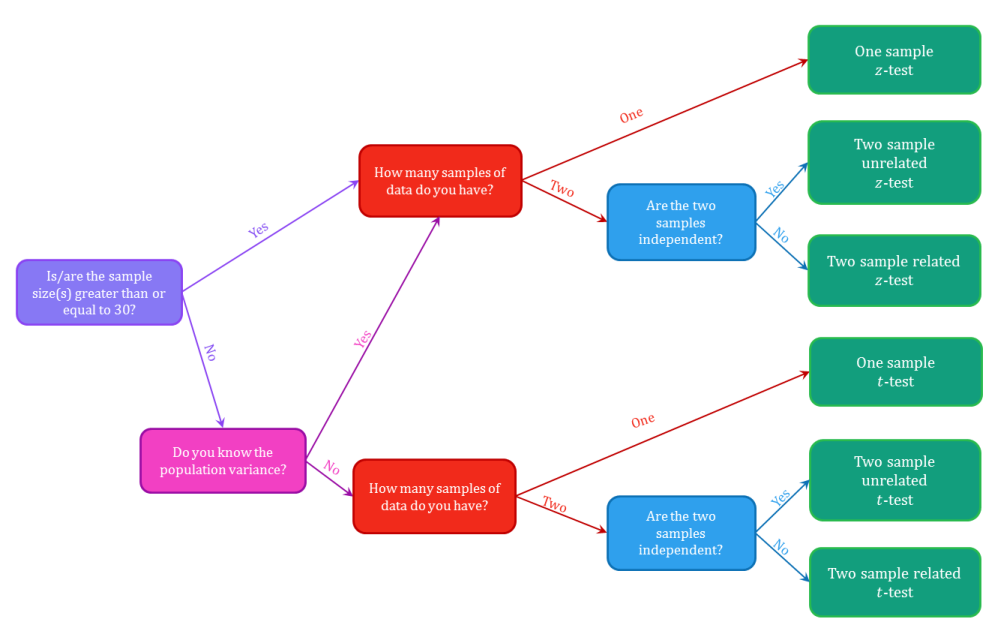
- When using two sample tests, you need to make sure the population variances are equal. SPSS will work this out for you, but to test for equal population variances by hand, you use an $F$-test.
- If your data is in the form of frequencies then you use a Chi-Squared test.
- If your data is non-Normal then you use a non-parametric test.
Test Yourself
Try our Numbas tests on parametric hypothesis tests and two-sample tests.
See Also
Click here for some more worked examples (from the Business page).
See also non-parametric hypothesis testing and tests on frequencies for information on other types of hypothesis testing.